
如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连接AP、CE.
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当 =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当 =n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
=n(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求 的值.
的值.

(1)证明见解析
?证明见解析
?n+1
【解析】
试题分析:(1)由BC垂直于l1可得∠ABP=∠CBE,由SAS即可证明;
(2)①延长AP交CE于点H,由(1)及已知条件可得AP⊥CE,△CPD∽△BPE,从而有DP=PE,得出四边形BDCE是平行四边形,从而可得到CE//BD,问题得证;
②由已知条件分别用S表示出△PAD和△PCE的面积,代入即可.
试题解析:(1)∵BC⊥直线l1,
∴∠ABP=∠CBE,
在△ABP和△CBE中
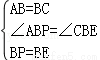
∴△ABP≌△CBE(SAS);
(2)①延长AP交CE于点H,
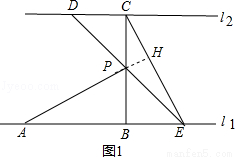
∵△ABP≌△CBE,
∴∠PAB=∠ECB,
∴∠PAB+∠AEE=∠ECB+∠AEH=90°,
∴AP⊥CE,
∵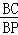 =2,即P为BC的中点,直线l1//直线l2,
=2,即P为BC的中点,直线l1//直线l2,
∴△CPD∽△BPE,
∴ =
=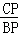 =
= ,
,
∴DP=PE,
∴四边形BDCE是平行四边形,
∴CE//BD,
∵AP⊥CE,
∴AP⊥BD;
②∵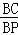 =N
=N
∴BC=n•BP,
∴CP=(n﹣1)•BP,
∵CD//BE,
∴△CPD∽△BPE,
∴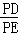 =
=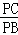 =n﹣1,
=n﹣1,
即S2=(n﹣1)S,
∵S△PAB=S△BCE=n•S,
∴S△PAE=(n+1)•S,
∵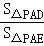 =
=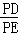 =n﹣1,
=n﹣1,
∴S1=(n+1)(n﹣1)•S,
∴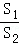 =
=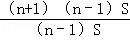 =n+1.
=n+1.
考点:1、全等三角形的性质与判定;2、相似三角形的性质与判定;3、平行四边形的性质与判定


科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:解答题
2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:选择题
某市约有4500000人,该数用科学记数法表示为( )
A.0.45×107 B.4.5×106 C.4.5×105 D.45×105
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:选择题
小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,其三视图如图,则n的值是( )
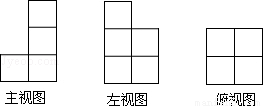
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:解答题
阳光中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题:
(1)若该社区有居民900人,试估计对消防知识“特别熟悉”的居民人数;
(2)该社区的管理人员有男、女个2名,若从中选2名参加消防知识培训,试用列表或画树状图的方法,求恰好选中一男一女的概率.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川甘孜卷)数学(解析版) 题型:选择题
在平面直角坐标系中,反比例函数y= 的图象的两支分别在( )
的图象的两支分别在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com