
 =0有实数根的概率.
=0有实数根的概率.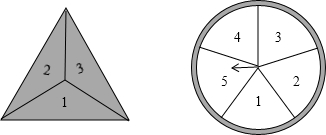
 ;
;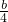 =0有实数根的条件为:9-ab≥0,
=0有实数根的条件为:9-ab≥0,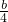 =0有实数根的概率为:
=0有实数根的概率为: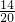 =
= .
.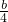 =0有实数根的所有情况,利用概率公式求解即可求得答案.
=0有实数根的所有情况,利用概率公式求解即可求得答案.

科目:初中数学 来源: 题型:
 0)和点B.
0)和点B.查看答案和解析>>
科目:初中数学 来源: 题型:
| b | 4 |

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:解答题
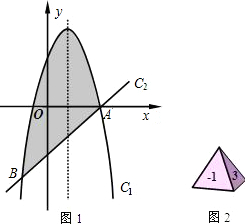
随机抛掷图中均匀的正四面体(正四面体的各面依次标有1,2,3,4四个数字),并且自由转动图中的转盘(转盘被分成面积相等的五个扇形区域).

(1)求正四面体着地的数字与转盘指针所指区域的数字之积为4的概率;
(2)设正四面体着地的数字为a,转盘指针所指区域内的数字为b,求关于x的方程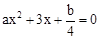 有实数根的概率.
有实数根的概率.
查看答案和解析>>
科目:初中数学 来源:2013年黑龙江省大庆市中考数学试卷 (解析版) 题型:解答题
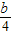 =0有实数根的概率.
=0有实数根的概率.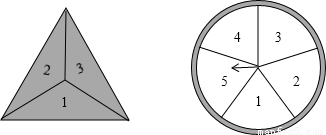
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com