解:(1)∵点D的坐标为(2,0),即OD=2,∠ADC=60°,∠COD=90°,
∴OC=OD•tan60°=2

,∠OCD=30°,
∴DC=2OD=4,
∴点C的坐标为(0,2

),
∵AB=BC=CD,
∴BC=4,AB=4,
过点B作BF⊥AD于点F,
∵BC∥AD,
∴BF=CO=2

,
∴点B的坐标为(-4,2

);
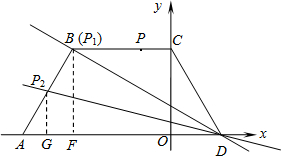
(2)当t=4时,CP=4,此时点P恰好与点B重合,记点P为P
1,
设直线DP
1的函数表达式为y=kx+b,
将B和D的坐标代入y=kx+b得:
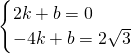
,
解得:
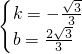
,
∴直线DP
1的函数表达式为y=-

x+

,S
△DCP1=

•BC•OC=

×4×2

=4

;
(3)由(1)知:AF=AB•cos60°=4×

=2,OF=BC=4,
∴AD=AF+OF+OD=8,
∴S
梯形ABCD=

×(4+8)×2

=12

,
(i)当点P在BC上时,由(2)知,当t=4时,S
△DCP1=4

=

S
梯形ABCD,
∴当t=4时,直线DP
1将梯形ABCD分成面积比为1:2的两部分;
(ii)当点P在AB上时,记点P为P
2,过点P
2作P
2G⊥AD于点G,
若S
△DCP2=

S
梯形ABCD=

×12

=4

,
则

×AD×P
2G=4

,又AD=8,
∴P
2G=

,
∴P
2A=
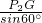
=
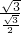
=2,
∴CB+BP
2=AB+BC-P
2A=4+4-2=6,
此时t=6,
综上,当t=4或t=6时,直线DP恰好将梯形ABCD分成面积比为1:2的两部分.
分析:(1)由D的坐标得出OD的长,在直角三角形OCD中,由∠ADC=60°,利用锐角三角函数定义及特殊角的三角函数值求出OC的长,得出C的坐标,且求出∠OCD=30°,利用直角三角形中,30°角所对的直角边等于斜边的一半求出CD的长,再由BC=CD=AB,得出CD与AB的长,过B作BF垂直于x轴,在直角三角形ABF中,由AB及∠BAD=60°,利用锐角三角函数定义及特殊角的三角函数值求出BF的长,由BC及BF即可得到B的坐标;
(2)当t=4时,根据每秒1个单位,求出CP=4,而BC=4,此时P与B重合,故设此时直线PD的解析式为y=kx+b,将B和D的坐标代入,得到关于k与b的方程组,求出方程组的解得到k与b的值,确定出直线PD的解析式,三角形DCP以BC为底边,BC边上的高与OC相等,利用三角形的面积公式即可求出三角形DCP的面积;
(3)由BF=OC,OF=BC,利用AD=AF+OF+OD求出AD,然后由上底BC,下底AD及高OC,求出梯形ABCD的面积,分两种情况考虑:(i)P在BC边上时,由(2)求出的三角形DCP面积恰好等于梯形面积的

,得到此时P与B重合,把P记作P
1,可得出t=4时,直线DP
1恰好将梯形ABCD分成面积比为1:2的两部分;(ii)当P在AB边上时,P记作P
2,过P
2作P
2G垂直于x轴,三角形AP
2D的面积以AD为底边,高为P
2G,根据三角形AP
2D的面积为梯形面积的

,列出关系式,求出P
2G的长,在直角三角形AP
2G中,由∠BAD=60°,利用锐角三角函数定义及特殊角的三角函数值求出AP
2的长,再由AB+BC-AP求出P
2运动的路程,即可求出此时的时间t,综上,得到所有满足题意的时间t的值.
点评:此题考查了坐标与图形性质,锐角三角函数定义,含30°直角三角形的性质,等腰梯形的性质,以及利用待定系数法求一次函数解析式,利用了数形结合及分类讨论的思想,是一道综合性较强的试题.

 停止,设运动时间为t秒.
停止,设运动时间为t秒. ,∠OCD=30°,
,∠OCD=30°, ),
), ,
, );
);
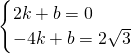 ,
,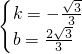 ,
, x+
x+ ,S△DCP1=
,S△DCP1= •BC•OC=
•BC•OC= ×4×2
×4×2 =4
=4 ;
; =2,OF=BC=4,
=2,OF=BC=4, ×(4+8)×2
×(4+8)×2 =12
=12 ,
, =
= S梯形ABCD,
S梯形ABCD, S梯形ABCD=
S梯形ABCD= ×12
×12 =4
=4 ,
, ×AD×P2G=4
×AD×P2G=4 ,又AD=8,
,又AD=8, ,
,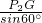 =
=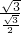 =2,
=2, ,得到此时P与B重合,把P记作P1,可得出t=4时,直线DP1恰好将梯形ABCD分成面积比为1:2的两部分;(ii)当P在AB边上时,P记作P2,过P2作P2G垂直于x轴,三角形AP2D的面积以AD为底边,高为P2G,根据三角形AP2D的面积为梯形面积的
,得到此时P与B重合,把P记作P1,可得出t=4时,直线DP1恰好将梯形ABCD分成面积比为1:2的两部分;(ii)当P在AB边上时,P记作P2,过P2作P2G垂直于x轴,三角形AP2D的面积以AD为底边,高为P2G,根据三角形AP2D的面积为梯形面积的 ,列出关系式,求出P2G的长,在直角三角形AP2G中,由∠BAD=60°,利用锐角三角函数定义及特殊角的三角函数值求出AP2的长,再由AB+BC-AP求出P2运动的路程,即可求出此时的时间t,综上,得到所有满足题意的时间t的值.
,列出关系式,求出P2G的长,在直角三角形AP2G中,由∠BAD=60°,利用锐角三角函数定义及特殊角的三角函数值求出AP2的长,再由AB+BC-AP求出P2运动的路程,即可求出此时的时间t,综上,得到所有满足题意的时间t的值.


 梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为
梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为