
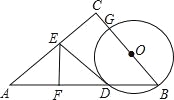
【题目】如图,在△ABC中,∠ACB=90°,AB=10,cosB=![]() ,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.
,G为BC上一点(不与B重合),以BG为直径的圆O交AB于D,作AD的垂直平分线交AD于F,交AC于E,连结DE.
(1)求证:DE为⊙O的切线;
(2)若BG=3,求DE的长;
(3)设BG=x,DE=y,求y与x的函数关系,写出y的最小值.
【答案】(1)、证明过程见解析;(2)、![]() ;(3)、y与x的函数关系是y=
;(3)、y与x的函数关系是y=![]() ,(0<x≤6),y的最小值是4.
,(0<x≤6),y的最小值是4.
【解析】
试题分析:(1)、连接OD、DG,由BG为圆的直径可知∠BDG是直角,然后只要证明∠ODE=90°,即可证明结论成立,根据题目中的条件可以得到∠ODE=90°,本题得以解决;(2)、根据题目中的条件和勾股定理,可以转化为直角三角形ODE和直角三角形OCD两直角边的平方等于OE的平方,从而可以得到DE的长;(3)、根据(2)中的求解方法,可以得到y与x的函数关系式,根据一次函数的性质,可以得到y的最小值.
试题解析:(1)、连接OD、DG,如右图所示, ∵BG为⊙O的直径,OD=OB,∠ACB=90°,
∴∠BDG=90°,∠ODB=∠B,∠B+∠A=90°, ∴∠A=∠ODG,∠GDE+∠EDA=90°,
又∵EF是AD的垂直平分线, ∴∠A=∠EDA, ∴∠EDA=∠ODG, ∴∠GDE+∠ODG=90°,
即OD⊥DE, ∵OD是⊙O的半径, ∴DE为⊙O的切线;
(2)、连接OE,如右上图所示,
∵∠ACB=90°,AB=10,cosB=![]() , ∴BC=ABcosB=6,AC=8, ∵BG=3,
, ∴BC=ABcosB=6,AC=8, ∵BG=3,
∴OD=1.5,OC=BC﹣OB=6﹣1.5=4.5, ∵EF是AD的垂直平分线, ∴EA=ED,
设EA=x,则ED=x,EC=8﹣x, ∵∠ECO=90°,∠EDO=90°, ∴DE2+OD2=EC2+OC2,
即x2+1.52=(8﹣x)2+4.52, 解得,x=![]() , 即DE的长是
, 即DE的长是![]() ;
;
(3)、连接OE,如右上图所示,
∵∠ACB=90°,AB=10,cosB=![]() , ∴BC=ABcosB=6,AC=8, ∵BG=x,
, ∴BC=ABcosB=6,AC=8, ∵BG=x,
∴OD=0.5x,OC=BC﹣OB=6﹣0.5x, ∵EF是AD的垂直平分线,ED=y, ∴EA=ED=y, ∴EC=8﹣y,
∵∠ECO=90°,∠EDO=90°, ∴DE2+OD2=EC2+OC2, 即y2+(0.5x)2=(8﹣y)2+(6﹣0.5x)2,
化简,得y=![]() ,(0<x≤6) ∵﹣
,(0<x≤6) ∵﹣![]() <0, ∴y随x的增大而减小,
<0, ∴y随x的增大而减小,
∴当x=6时,y取得最小值,此时y=![]() =4, 即y与x的函数关系是y=
=4, 即y与x的函数关系是y=![]() ,(0<x≤6),y的最小值是4.
,(0<x≤6),y的最小值是4.



 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图是芳芳设计的自由转动的转盘,上面写有10个有理数。想想看,转得下列各数的概率是多少?
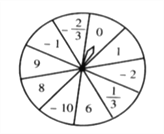
(1)转得正数;
(2)转得正整数;
(3)转得绝对值小于6的数;
(4)转得绝对值大于等于8的数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索题:
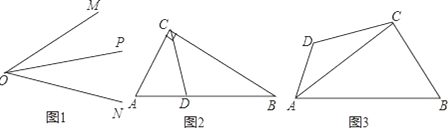
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,交射线ON,OM为C,B两点,在射线OP上任取一点A(O点除外),连接AB,AC,求证:△AOB≌△AOC.
(2)请你参考这个作全等三角形的方法,解答下列问题:
①如图2:在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系;
②如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各数中,是近似数的是( )。
A.七(1)班共有65名同学
B.足球比赛每方共有11名球员
C.光速是300000000米/秒
D.小王比小华多2元
查看答案和解析>>
科目:初中数学 来源: 题型:
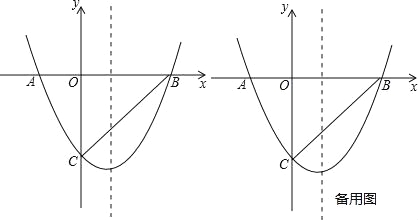
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0)和点B(4,0),与y轴交于点C(0,﹣4).
(1)求二次函数的解析式,并写出抛物线的对称轴,顶点坐标;
(2)设E时抛物线对称轴上一点,当∠BEC=90°时,求点E的坐标;
(3)若P(m,n)是抛物线上一个动点(其中m>0,n<0),是否存在这样的点P,使得△PBC的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车 间生产一批圆柱形机器零件,从中抽出了 6 件进行检验,把标准直径的长记为 0,比标准直径长的记为正数,比标准直径短的记为负数,检查记录如下:
1 | 2 | 3 | 4 | 5 | 6 |
+0.2 | ﹣0.3 | ﹣0.2 | +0.3 | +0.4 | ﹣0.1 |
则第_________个零件最符合标准.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com