
已知二次函数y=mx2+nx+p图象的顶点横坐标是2,与x轴交于A(x1,0),B(x2,0),x1<0<x2,与y轴交于点C,O为坐标原点,tan∠CAO-tan∠CBO=1.
(1)求证:n+4m=0;
(2)求m,n的值;
(3)当p>0且二次函数图象与直线y=x+3仅有一个交点时,求二次函数的最大值.
(1)证明:∵二次函数y=mx2+nx+p图象的顶点横坐标是2,
∴抛物线的对称轴为x=2,即-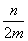 =2,
=2,
化简,得n+4m=0.
(2)解:∵二次函数y=mx2+nx+p与x轴交于A(x1,0),B(x2,0),x1<0<x2,
∴OA=-x1,OB=x2,x1+x2=-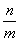 ,x1·x2=
,x1·x2=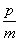 .
.
令x=0,得y=p,∴C(0,p).∴OC=|p|.
由三角函数定义,得tan∠CAO= =-
=- ,tan∠CBO=
,tan∠CBO=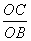 =
=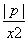 .
.
∵tan∠CAO-tan∠CBO=1,即- -
-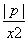 =1.
=1.
化简,得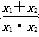 =
=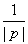 .
.
将x1+x2=-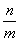 ,x1·x2=
,x1·x2=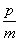 代入,得
代入,得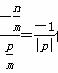 化简,得⇒n=
化简,得⇒n=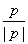 =±1.
=±1.
由(1)知n+4m=0,
∴当n=1时,m=-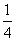 ;当n=-1时,m=
;当n=-1时,m=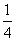 .
.
∴m,n的值为:m=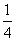 ,n=-1(此时抛物线开口向上)或m=-
,n=-1(此时抛物线开口向上)或m=-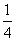 ,n=1(此时抛物线开口向下).
,n=1(此时抛物线开口向下).
(3)解:由(2)知,当p>0时,n=1,m=-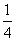 ,
,
∴抛物线解析式为:y=-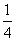 x2+x+p.
x2+x+p.
联立抛物线y=-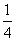 x2+x+p与直线y=x+3解析式得到-
x2+x+p与直线y=x+3解析式得到-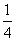 x2+x+p=x+3,
x2+x+p=x+3,
化简,得x2-4(p-3)=0.
∵二次函数图象与直线y=x+3仅有一个交点,
∴一元二次方程根的判别式等于0,
即Δ=02+16(p-3)=0,解得p=3.
∴y=-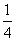 x2+x+3=-
x2+x+3=-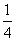 (x-2)2+4.
(x-2)2+4.
当x=2时,二次函数有最大值,最大值为4.


科目:初中数学 来源: 题型:
抛物线y=x2+bx+c的图象先向右平移2个单位长度,再向下平移3个单位长度,所得图象的函数解析式为y=(x-1)2-4,则b,c的值为( )
A.b=2,c=-6 B.b=2,c=0 C.b=-6,c=8 D.b=-6,c=2
查看答案和解析>>
科目:初中数学 来源: 题型:
由一些大小相同的小正方体搭成的几何体的左视图和俯视图如图6225所示,则搭成该几何体的小正方体的个数最少是( )
A.4个 B.5个 C.6个 D.7个

查看答案和解析>>
科目:初中数学 来源: 题型:
在一副扑克牌中,拿出红桃2、红桃3、红桃4、红桃5四张牌,洗匀后,小明从中随机摸出一张,记下牌面上的数字为x,然后放回并洗匀,再由小华随机摸出一张,记下牌面上的数字为y,组成一对数(x,y).
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com