
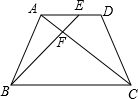
 在等腰梯形ABCD中,AD∥CB,且AD=
在等腰梯形ABCD中,AD∥CB,且AD=| 1 |
| 2 |
| S△AEF |
| S△CBF |
科目:初中数学 来源: 题型:
| A、2.58×107 |
| B、0.258×107 |
| C、25.8×106 |
| D、2.58×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:
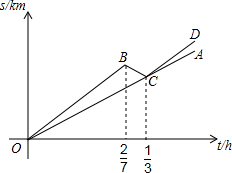 某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.
某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com