
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 2sinA-3=0 | B. | cos2B=1 | C. | tan B+1=0 | D. | tan2 A=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
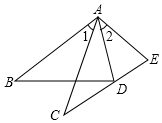 在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
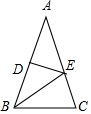 如图,在△ABC中,AB=AC=9cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.若BC=6cm,则△BCE的周长是15 cm.
如图,在△ABC中,AB=AC=9cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.若BC=6cm,则△BCE的周长是15 cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
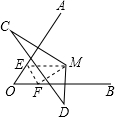 如图,OA、OB分别是线段MC、MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短可为( )
如图,OA、OB分别是线段MC、MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短可为( )| A. | 12cm | B. | 10cm | C. | 7cm | D. | 5cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com