
【题目】如图,直线EF与⊙O相切于点C,点A为⊙O上异于点C的一动点,⊙O的半径为4,AB![]() EF于点B,设
EF于点B,设![]() ACF=α(0°<α<180°).
ACF=α(0°<α<180°).
(1)若α=![]() ,求证:四边形OCBA为正方形;
,求证:四边形OCBA为正方形;
(2)若AC―AB=1,求AC的长;
(3)当AC―AB取最大值时,求α的度数.
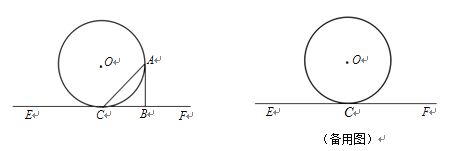
【答案】(1)见解析;(2)AC=![]() ;(3)∠α=
;(3)∠α=![]() 或
或![]()
【解析】
(1)连接OA,OC,证△ABC是等腰直角三角形,△OAC是等腰直角三角形,再证四边形OCBA为矩形
由OA=OC,得四边形OCBA为正方形;(2)作OH![]() AB,设AC=x,则AB=x-1,由勾股定理得,在Rt△OAH中,
AB,设AC=x,则AB=x-1,由勾股定理得,在Rt△OAH中,![]() ,在Rt△OEC中,
,在Rt△OEC中,![]() ,
,![]() ;(3)根据锐角三角函数和相似三角形性质可得出差的函数解析式,再求最值.
;(3)根据锐角三角函数和相似三角形性质可得出差的函数解析式,再求最值.
解:(1)连接OA,OC
∵α=![]() ,AB
,AB![]() EF
EF
∴△ABC是等腰直角三角形
∵EF与⊙O相切于C
∴∠OCB=![]()
∴∠OCA=![]()
∴△OAC是等腰直角三角形
∴∠OCB=∠CBA=∠COA=900
∴四边形OCBA为矩形
∵OA=OC
∴四边形OCBA为正方形
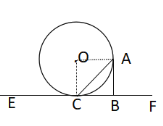
(2)如图,作OH⊥AB,
设AC=x,则AB=x-1

∵在Rt△OAH中,![]()
又∵在Rt△OEC中,![]()
∴![]()
∴![]()
即:AC=![]()
(3)如图,作OH⊥AC,则AC=2CH,设CH=x,AC=2x,
由(1)(2)可得
![]()
∴![]() ,即
,即![]()
∴AB=![]()
∴AC-AB=y=2x-![]() ,∵当x=2时,y最大.
,∵当x=2时,y最大.
此时,sinα=![]()
∴α=300
同理,当A在OC的左侧时,α=1500,AC-AB的值最大.
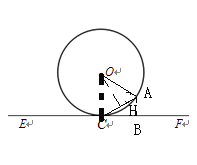
∴当AC-AB取最大值时,![]() α=
α=![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】某乒乓球馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费;②银卡售价150元/张,每次凭卡另收10元;暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设打乒乓x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图像如图所示,请根据函数图像,写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市教育教学研究室为了了解该市所有毕业班学生参加2019年安徽省中考一模考试的数学成绩情况(满分:150分,等次:![]() 等,130分
等,130分![]() 150分;
150分;![]() 等,110分
等,110分![]() 129分;C等,90分
129分;C等,90分![]() 109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
2019年合肥市一模数学成绩频数分布表
等次 | 频数 | 频率 |
| 0.2 | |
| ||
| 6 | |
| 2 | 0.1 |
合计 | 1 |
2019年合肥市一模教学成绩频数分布直方图
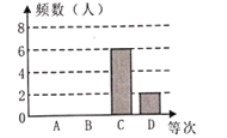
根据图表中的信息,下列说法不正确的是( )
A. 这次抽查了20名学生参加一模考试的数学成绩
B. 这次一模考试中,考试数学成绩为![]() 等次的频率为0.4
等次的频率为0.4
C. 根据频数分布直方图制作的扇形统计图中等次![]() 所占的圆心角为
所占的圆心角为![]()
D. 若全市有20000名学生参加中考一模考试,则估计数学成绩达到![]() 等次及以上的人数有12000人
等次及以上的人数有12000人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向下的抛物线y=ax2-2ax+2与y轴的交点为A,顶点为B,对称轴与x轴的交点为C,点A与点D关于对称轴对称,直线BD与x轴交于点M,直线AB与直线OD交于点N.
(1)求点D的坐标.
(2)求点M的坐标(用含a的代数式表示).
(3)当点N在第一象限,且∠OMB=∠ONA时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省计划5年内全部地级市通高铁.某高铁在泰州境内的建设即将展开,现有大量的沙石需要运输.某车队有载质量为8t、10t的卡车共12辆,全部车辆运输一次能运输100t沙石.
(1)求某车队载质量为8t、10t的卡车各有多少辆;
(2)随着工程的进展,某车队需要一次运输沙石165t以上,为了完成任务,准备新增购这两种卡车共7辆,车队有多少种购买方案?请你一一求出.
查看答案和解析>>
科目:初中数学 来源: 题型:
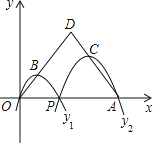
【题目】如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种乐器有10个孔,依次记作第1孔,第2孔,……,第10孔,演奏时,第n孔与其音色的动听指数D之间满足关系式![]() ,该乐器的最低动听指数为4k+106,求常数k的取值范围。
,该乐器的最低动听指数为4k+106,求常数k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
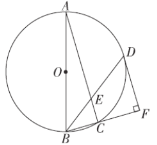
【题目】如图,AB是⊙O的直径,△ABC内接于⊙O.点D在⊙O 上,BD平分∠ABC交AC于点E,DF⊥BC交BC的延长线于点F.
(1)求证:FD是⊙O的切线;
(2)若BD=8,sin∠DBF=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以80海里/小时的速度继续航行多少小时即可到达?(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com