
【题目】求证:两边分别相等且其中一组等边的对角相等的两个锐角三角形全等.
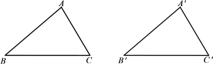
【答案】答案见解析
【解析】
画出图形,结合图形写出已知、求证,然后证明即可.
过点A作AD⊥BC于点D,过点A′ 作A′D′⊥B′C′于点D′,先证明△ACD≌△A′C′D′,得到AD= A′D′.再证明Rt△ABD≌Rt△A' B' D',得到∠B =∠B'.最后证明△ABC≌△A' B' C'即可.
已知:如图,在锐角三角形ABC和锐角三角形△A′B′C′中,AB=A′B′,AC= A′C′,∠C=∠C′.
求证:△ABC≌△A′B′C′.

证明:过点A作AD⊥BC于点D,过点A′ 作A′D′⊥B′C′于点D′,∴∠ADC=∠A′D′C′=∠ADB=∠A′D′B′=90°.
在△ACD和△A′C′D′中,∵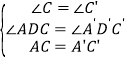 ,∴△ACD≌△A′C′D′(AAS),∴AD= A′D′.
,∴△ACD≌△A′C′D′(AAS),∴AD= A′D′.
在![]() △ABD和Rt△A′B′D′中,∵
△ABD和Rt△A′B′D′中,∵![]() ,∴Rt
,∴Rt![]() ≌Rt
≌Rt![]() (HL),∴∠
(HL),∴∠![]()
![]() ∠
∠![]() .
.
在△ABC和△A' B' C' 中,∵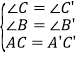 ,∴
,∴![]() ≌
≌![]() (AAS).
(AAS).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个) 
查看答案和解析>>
科目:初中数学 来源: 题型:
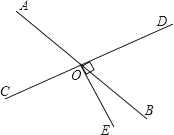
【题目】如图,AB和CD相交于点O,∠DOE=90°,若∠BOE=![]() ∠AOC,
∠AOC,
(1)指出与∠BOD相等的角,并说明理由.
(2)求∠BOD,∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,引射线OC(点C在∠AOB外),OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=40°,请依题意补全图,并求∠BOE的度数;
(2)若∠BOC=α(0°<α<180°),请直接写出∠BOE的度数(用含α的代数式表示).
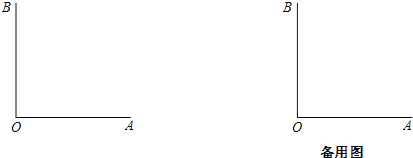
查看答案和解析>>
科目:初中数学 来源: 题型:
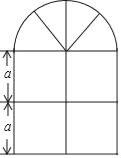
【题目】如图,某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆内部用了三根等长的木条分隔,下部是用木条围成的边长相同的四个小正方形,木条宽厚不计,已知下部的小正方形的边长为a米.
(1)用含a的式子分别表示窗户的面积和木条用料(实线部分)的总长;
(2)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,木条每米20元,求制作这扇窗户需要多少元?(π取3,结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,2)在反比例函数y= ![]() (x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
(x>0)上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为( )
A.(2,1)
B.(3, ![]() )
)
C.(4,0.5)
D.(5,0.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD和△ACE分别是等边三角形,AB≠AC,下列结论中正确有( )个.(1)DC=BE,(2)∠BOD=60°,(3)∠BDO=∠CEO,(4)AO平分∠DOE,(5)AO平分∠BAC.
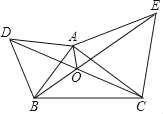
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y= ![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD= ![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.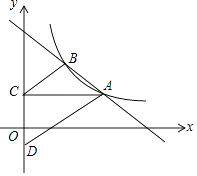
(1)求m,k,n的值;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com