
【题目】如图,在平面直角坐标系中,直线AB与函数y= ![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD= ![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.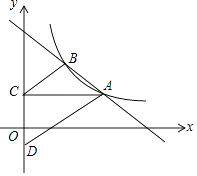
(1)求m,k,n的值;
(2)求△ABC的面积.
【答案】
(1)解:∵点A的坐标为(m,2),AC平行于x轴,
∴OC=2,AC⊥y轴,
∵OD= ![]() OC,
OC,
∴OD=1,
∴CD=3,
∵△ACD的面积为6,
∴ ![]() CDAC=6,
CDAC=6,
∴AC=4,即m=4,
则点A的坐标为(4,2),将其代入y= ![]() 可得k=8,
可得k=8,
∵点B(2,n)在y= ![]() 的图象上,
的图象上,
∴n=4;
(2)解:如图,过点B作BE⊥AC于点E,则BE=2,
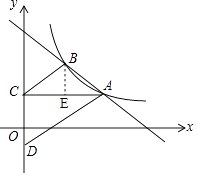
∴S△ABC= ![]() ACBE=
ACBE= ![]() ×4×2=4,
×4×2=4,
即△ABC的面积为4.
【解析】由AC平行,可得A、C的纵坐标相等,等于2,再由OD= ![]() OC,可得CD=3,由面积可求得AC=4,即m=4,进而求得n=4,k=8;(2)△ABC是水平三角形,可选择水平边AC作为底边,需过B作出AC边上的高,求出高即可求出面积.
OC,可得CD=3,由面积可求得AC=4,即m=4,进而求得n=4,k=8;(2)△ABC是水平三角形,可选择水平边AC作为底边,需过B作出AC边上的高,求出高即可求出面积.


科目:初中数学 来源: 题型:
【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.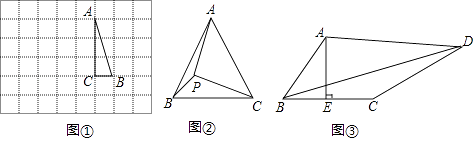
(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
(3)【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
(4)【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
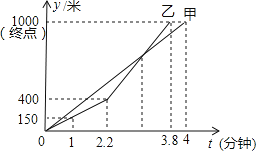
【题目】端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程![]() 米
米![]() 与时间
与时间![]() 分钟
分钟![]() 之间的函数关系图象如图所示,请你根据图象,回答下列问题:
之间的函数关系图象如图所示,请你根据图象,回答下列问题:
![]() 这次龙舟赛的全程是______ 米,______ 队先到达终点;
这次龙舟赛的全程是______ 米,______ 队先到达终点;
![]() 求乙与甲相遇时乙的速度;
求乙与甲相遇时乙的速度;
![]() 求出在乙队与甲相遇之前,他们何时相距100米?
求出在乙队与甲相遇之前,他们何时相距100米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】说明理由
如图,∠1+∠2=230°,b∥c, 则∠1、∠2、∠3、∠4各是多少度?

解:∵ ∠1=∠2 (_________________________)
∠1+∠2=230°
∴∠1 =∠2 =________(填度数)
∵ b∥c
∴∠4 =∠2= ________(填度数)
( )
∠2 +∠3 =180° ( )
∴∠3 =180°-∠2 =_________(填度数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是__________(只需填写正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示: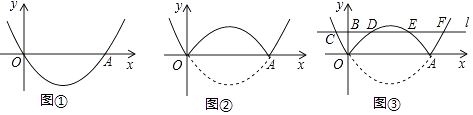
(1)【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣ ![]() 经过原点O,与x轴的另一个交点为A,则a= .
经过原点O,与x轴的另一个交点为A,则a= .
(2)【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.
(3)【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.
(4)【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.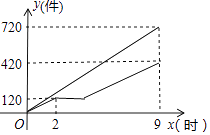
(1)甲车间每小时加工服装件数为件;这批服装的总件数为件.
(2)求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;
(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com