
【题目】如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是__________(只需填写正确结论的序号).

【答案】①③④
【解析】
①由等边三角形的性质得出∠EAF=60°,AE=AF,求出∠C=120°,由平行四边形的性质得出AB∥CD,∠C=∠BAD=120°,得出∠B=180°-∠C=60°,①正确;
②由平行四边形的性质得出∠D=∠B=60°,求出∠BAE=∠DAF=30°,得出∠EAF=120°-30°-30°=60°,但是AE不一定等于AF,②错误;
③由平行四边形的面积得出![]() BCAE=
BCAE=![]() CDAF,得出BC=CD,证出平行四边形ABCD是菱形,③正确;
CDAF,得出BC=CD,证出平行四边形ABCD是菱形,③正确;
④由菱形的性质得出BC=CD,由面积得出![]() BCAE=
BCAE=![]() CDAF,得出AE=AF,④正确;即可得出结论.
CDAF,得出AE=AF,④正确;即可得出结论.
解:①∵△AEF是等边三角形,
∴∠EAF=60°,AE=AF,
又∵AE⊥BC,AF⊥CD,
∴∠C=120°,
∵四边形ABCD是平行四边形,
∴AB∥CD,∠C=∠BAD=120°,
∴∠B=180°-∠C=60°,故①正确;
②∵∠D=∠B=60°,
∴∠BAE=∠DAF=90°-60°=30°,
∴∠EAF=120°-30°-30°=60°,
但是AE不一定等于AF,故②错误;
③若AE=AF,则![]() BCAE=
BCAE=![]() CDAF,
CDAF,
∴BC=CD,
∴平行四边形ABCD是菱形,故③正确;
④若平行四边形ABCD是菱形,
则BC=CD,
∴![]() BCAE=
BCAE=![]() CDAF,
CDAF,
∴AE=AF,故④正确;
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2 016个三角形的周长为( )
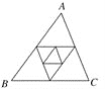
A. 22 016 B. 22 017 C. (![]() )2 016 D. (
)2 016 D. (![]() )2 015
)2 015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y= ![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD= ![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.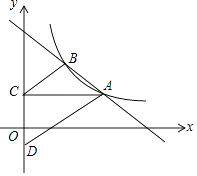
(1)求m,k,n的值;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③![]() ;④BD平分∠ADC;⑤∠BDC=
;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.其中正确的结论有_______个.
∠BAC.其中正确的结论有_______个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.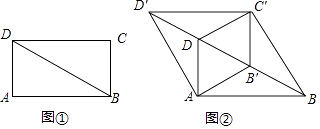
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是 ,依次继续下去…,第2013次输出的结果是 .
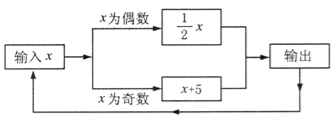
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4……,排列成如图1所示的一个表,从上到下分别称为第1行、第2行、…,从左到右分别称为第1列、第2列、…….用图2所示的方框在图1中框住16个数,把其中没有被阴影覆盖的四个数分别记为A、B、C、D.设A=x.

(1)在图1中,2018排在第 行第 列;排在第m行第n列的数为 ,其中m≥1,1≤n≤8,且都是正整数;(直接写出答案)
(2)若A+2B+3D=357,求出C所表示的数;
(3)在图(2)中,被阴影覆盖的这些数的和能否为4212?如果能,请求出这些数中最大的数,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com