
【题目】如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.

科目:初中数学 来源: 题型:
【题目】方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:

(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过![]() h与乙相遇,问丙出发后多少时间与甲相遇?
h与乙相遇,问丙出发后多少时间与甲相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演门票,他们决定采用抽卡片的办法确定谁去.规则如下:
将正面分别标有数字1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和为偶数,则小亮去.
(1)请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现的结果;
(2)你认为这个规则公平吗?请说明理由.
考点:游戏公平性;列表法与树状图法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如下图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为 ;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B',补全△A′B′C′;
(3)在图中画出△ABC的高CD;
(4)若连接![]() ,
, ![]() ,则这两条线段之间的关系是 ;
,则这两条线段之间的关系是 ;
(5)能使S△ABC=S△QBC的格点Q,共有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富群众文化生活,某县城区已经整体转换成了数字电视.目前该县广播电视信息网络公司正在对乡镇进行数字电视改装.公司现有400户申请了但还未安装的用户,此外每天还有新的用户申请.已知每个安装小组每天安装的数量相同,且每天申请安装的用户数也相同,公司若安排3个安装小组同时安装,则50天可以安装完所有新、旧申请用户;若公司安排5个安装小组同时安装,则10天可以安装完所有新,旧申请用户.
(1)求每天新申请安装的用户数及每个安装小组每天安装的数量;
(2)如果要求在8天内安装完所有新、旧申请用户,但前3天只能派出2个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:善于思考的小军在解方程组![]()
![]() 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解:将方程②变形为4x+10y+y=5,即2(2x+5y)+y=5, ③
把方程①代入③得2×3+y=5,∴y=-1,
把y=-1代入①得x=4,
∴方程组的解为![]()
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组![]()
![]()
(2)已知x,y满足方程组![]()
![]() 求整式x2+4y2+xy的值;
求整式x2+4y2+xy的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.
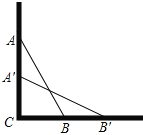
(1)这云梯的顶端距地面AC有多高?
(2)如果云梯的顶端A下滑了4米,那么它的底部B在水平方向向右滑动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
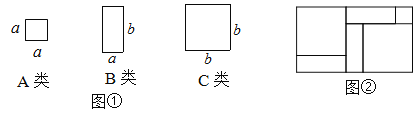

(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+b)、(a+2b),不画图形,试通过计算说明需要C类卡片多少张;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积等于a2+5ab+4b2,画出这个长方形,并根据图形对多项式a2+5ab+4b2进行因式分解;
(3) 如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案并判断,将正确关系式的序号填写在横线上______ _____(填写序号)
①.xy =![]() ②.x+y=m ③.x2-y2=m·n ④.x2+y2 =
②.x+y=m ③.x2-y2=m·n ④.x2+y2 =![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com