
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .


y=2x .
【考点】相似三角形的性质;反比例函数图象上点的坐标特征.
【专题】数形结合.
【分析】设OC=a,根据点D在反比例函数图象上表示出CD,再根据相似三角形对应边成比例列式求出AC,然后根据中点的定义表示出点B的坐标,再根据点B在反比例函数图象上表示出a、k的关系,然后用a表示出点B的坐标,再利用待定系数法求一次函数解析式解答.
【解答】解:设OC=a,
∵点D在y=
 上,
上,
∴CD=
 ,
,
∵△OCD∽△ACO,
∴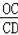
 =
=
 ,
,
∴AC=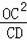
 =
=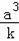
 ,
,
∴点A(a,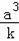
 ),
),
∵点B是OA的中点,
∴点B的坐标为(
 ,
,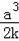
 ),
),
∵点B在反比例函数图象上,
∴
 =
=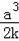
 ,
,
∴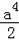
 =2k2,
=2k2,
∴a4=4k2,
解得,a2=2k,
∴点B的坐标为(
 ,a),
,a),
设直线OA的解析式为y=mx,
则m•
 =a,
=a,
解得m=2,
所以,直线OA的解析式为y=2x.
故答案为:y=2x.
【点评】本题考查了相似三角形的性质,反比例函数图象上点的坐标特征,用OC的长度表示出点B的坐标是解题的关键,也是本题的难点.


科目:初中数学 来源: 题型:
对于函数y= - ,下列结论错误的是 ( )
,下列结论错误的是 ( )
A、当x>0时,y随x的增大而增大
B、当x<0时,y随x的增大而增大
C、当x=1时的函数值大于x= -1时的函数值
D、在函数图象所在的象限内,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两地之间的高速公路全长200千米,比原来国道的长度减少了20千米.高速公路通车后,某长途汽车的行驶速度提高了45千米/时,从甲地到乙地的行驶时间缩短了一半.设该长途汽车在原来国道上行驶的速度为x千米/时,根据题意,下列方程正确的是( )
A.
 B.
B.

C.
 D.
D.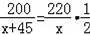

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC的面积为1.第一次操 作:分别延长AB,BC,CA至点A1,B1,C1,使
作:分别延长AB,BC,CA至点A1,B1,C1,使 A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操
A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操 作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=
作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1= A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过 次操作( )
A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过 次操作( )
A.3 B.4 C.5 D.6

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com