
【题目】如图,抛物线![]() 与y轴交于点A(0,-
与y轴交于点A(0,- ![]() ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
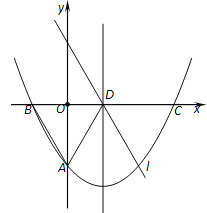
(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
【答案】(1)![]() (2)△ABD是等边三角形,(3)
(2)△ABD是等边三角形,(3)![]()
【解析】试题分析:(1)先求得抛物线的解析式,再求得点B、C的坐标,再由待定系数法求出直线AB的解析式;(2)△ABD是等边三角形,根据已知条件易证△BOA≌△DOA,可得BA=DA,根据锐角三角函数可求得∠ABO=60°,即可判定△ABD是等边三角形;(3)过点E作EG∥x轴,交AB于点G, 易证△AEG是等边三角形,可得AE=AG,再证△BEG≌△EFD,可得BE=EF,易得△BEF是等边三角形 ,当BE⊥AD时,BE的长度最小,则△BEF的面积取最小值,求得△BEF面积的最小值即可.
试题解析:
(1)将点A(0,- ![]() )代入抛物线解析式中,得c=-
)代入抛物线解析式中,得c=-![]() ,
,
![]()
![]()
当y=0时, ![]()
化简得x2-2x-3=0
![]() (x+1)(x-3)=0
(x+1)(x-3)=0
![]() x 1=-1, x 2=3
x 1=-1, x 2=3
![]() 点B (-1,0),点C(3,0)
点B (-1,0),点C(3,0)
设直线AB的表达式为y=kx+b,
![]() 图象经过点A(0,-
图象经过点A(0,- ![]() ),点B (-1,0),
),点B (-1,0),
代入得 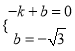 ,解得
,解得
![]() 直线AB的表达式为
直线AB的表达式为![]()
(2)△ABD是等边三角形,
![]() 点B(-1,0), 点D(1,0)
点B(-1,0), 点D(1,0)
![]() OB=OD=1,
OB=OD=1,
∵OA是公共边,∠BOA=∠DOA=90°,
∴△BOA≌△DOA,
∴BA=DA,
tan∠ABO=![]() ,
,
∴∠ABO=60°,
![]() △ABD是等边三角形
△ABD是等边三角形
(3)过点E作EG∥x轴,交AB于点G,
∵△ABD是等边三角形
∴∠BAD=∠ABD=∠ADB
∴∠AEG=∠AGE=60°
∴△AEG是等边三角形,
∴AE=AG
∴DE=BG
∵AB∥l
∴∠EDF=∠BGE=120°
∴∠GBE+∠GEB=60°,∠DEF+∠GEB=60°,
∴∠GBE=∠DEF
∴△BEG≌△EFD
∴BE=EF
又∵∠BEF=60°
∴△BEF是等边三角形
∴S△BEF=![]()
当BE⊥AD时,BE的长度最小,则△BEF的面积取最小值,
此时,BE=ABsin60°=![]() ,
,
△BEF面积的最小值=![]() =
=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,某校计划在早间校园广播台播放“百家讲坛”的部分内容,为了了解学生的喜好,随机抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下: 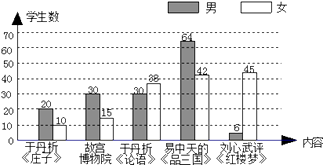
请根据统计图提供的信息回答以下问题:
(1)抽取的学生数为名;
(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有名;
(3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的%.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为了进一步普及卫生知识、提高卫生意识、推广健康生活,今年3月份举行了一次卫生知识竞赛,这次竞赛中共有20道题,每一题答对得5分,答错或不答都扣3分.
(1)小明考了68分,那么小明答对了多少道题?
(2)小亮获得二等奖(70分~90分),请你算算小亮答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统汁图,请根据图中信息解答下列问题:

(l)本次抽取样本容量为____,扇形统计图中A类所对的圆心角是____度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com