
【题目】如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
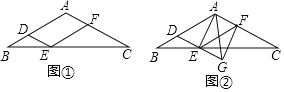
【答案】(1)证明见解析;(2)ADEF的形状为菱形,理由见解析;(3)四边形AEGF是矩形,理由见解析.
【解析】
(1)根据平行线的性质得到∠BDE=∠A,根据题意得到∠DEF=∠BDE,根据平行线的判定定理得到AD∥EF,根据平行四边形的判定定理证明;
(2)根据三角形中位线定理得到DE=![]() AC,得到AD=DE,根据菱形的判定定理证明;
AC,得到AD=DE,根据菱形的判定定理证明;
(3)根据等腰三角形的性质得到AE⊥EG,根据有一个角是直角的平行四边形是矩形证明.
(1)证明:∵DE∥AC,
∴∠BDE=∠A,
∵∠DEF=∠A,
∴∠DEF=∠BDE,
∴AD∥EF,又∵DE∥AC,
∴四边形ADEF为平行四边形;
(2)解:□ADEF的形状为菱形,
理由如下:∵点D为AB中点,
∴AD=![]() AB,
AB,
∵DE∥AC,点D为AB中点,
∴DE=![]() AC,
AC,
∵AB=AC,
∴AD=DE,
∴平行四边形ADEF为菱形,
(3)四边形AEGF是矩形,
理由如下:由(1)得,四边形ADEF为平行四边形,
∴AF∥DE,AF=DE,
∵EG=DE,
∴AF∥DE,AF=GE,
∴四边形AEGF是平行四边形,
∵AD=AG,EG=DE,
∴AE⊥EG,
∴四边形AEGF是矩形.
故答案为:(1)证明见解析;(2)菱形;(3)矩形.


科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的均匀转盘![]() ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘![]() ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).

【1】用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
【2】小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到永丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,![]() ,
,![]() .
.
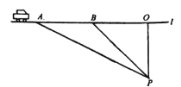
(1)求A、B之间的路程;
(2)请判断此车是否超过了永丰路每小时54千米的限制速度?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列的解题过程,然后回答下列问题.
例:解绝对值方程:![]() .
.
解:讨论:①当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() ;
;
②当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
原方程的解为![]() 或
或![]() .
.
(1)依例题的解法,方程算![]() 的解是_______;
的解是_______;
(2)尝试解绝对值方程:![]() ;
;
(3)在理解绝对值方程解法的基础上,解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”是中华民族每个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用![]() 、
、![]() 、
、![]() 、
、![]() 四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题.
四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题.
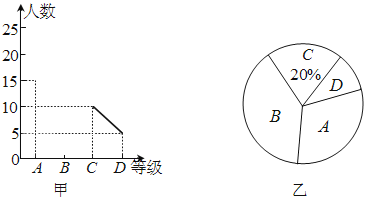
(1)共抽取了多少个学生进行调查?
(2)求![]() 、
、![]() 、
、![]() 等级的百分比.
等级的百分比.
(3)求出图乙中![]() 等级所占圆心角的度数.
等级所占圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
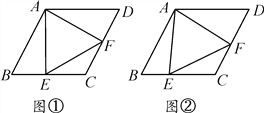
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某县结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见下表
一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
不超过150千瓦时的部分 | a |
超过150千瓦时,但不超过230千瓦时的部分 | b |
超过230千瓦时的部分 | a+0.33 |
2019年10月份,该县居民甲用电100千瓦时,交费64元;居民乙用电200千瓦时,交费134.5元.
(1)根据题意,求出上表中a和b的值;
(2)实行“阶梯电价”收费以后,该县居民当月用电多少千瓦时时,其当月的平均电价为0.67元?
查看答案和解析>>
科目:初中数学 来源: 题型:
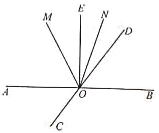
【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com