
����Ŀ����ͼ��������![]() ���ʾ��
���ʾ��![]() ��
��![]() ���ʾ��
���ʾ��![]() ����
����![]() ��
��![]() ����
����![]()
![]()
![]() ��
��![]() ��ʾ����Ϊ________����
��ʾ����Ϊ________����![]() ��ʾ����Ϊ________��
��ʾ����Ϊ________��
![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ��������������һ��
��������������һ��![]() ��ʹ
��ʹ![]() ����
����![]() ���ʾ����________��
���ʾ����________��
![]() ����ԭ��
����ԭ��![]() ����һ���壬һС��״ӵ�
����һ���壬һС��״ӵ�![]() ����
����![]() ����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�
����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�![]() ����
����![]() ����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊ
����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊ![]() ���룩����ֱ��ʾ���ס�����С��ԭ��ľ��루�ú�
���룩����ֱ��ʾ���ס�����С��ԭ��ľ��루�ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
���𰸡���1��-5��7����2��4��13����3����0��t��3.5ʱ��С��ԭ��ľ���Ϊ7��2t����t��3.5ʱС��ԭ��ľ���Ϊ2t��7��
��������
��1�����ݷǸ����������з������a��b��ֵ���Ӷ��ý⣻
��2��������������ı�ʾ�г�����ֵ���̣�Ȼ����⼴�ɣ�
��3����С����������ϵ����������ʾ���ɣ���С��������������ƶ��������ֱַ���ʽ��ʾ���ɣ�
��1��������ã�a+5=0��b��7=0��
���a=��5��b=7��
���ԣ���A��ʾ��5����B��ʾ7��
��2�����C��ʾx��������ã�|��5��x|=3|7��x|��
���ԣ�5+x=3��7��x����5+x=��3��7��x����
���x=4����x=13��
���ԣ���C��ʾ����Ϊ4��13��
��3���ף���С��״ӵ�A����1����λ/����ٶ������˶���
���ԭ��ľ���Ϊ|��5��t|=5+t��
��С���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶���
���ҵ���ԭ���ʱ��Ϊ7��2=3.5��
�൱0��t��3.5ʱ��С��ԭ��ľ���Ϊ7��2t��
��t��3.5ʱС��ԭ��ľ���Ϊ2t��7��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC ��AD = 9cm��BC = 6cm����P��Q�ֱ�ӵ�A��Cͬʱ��������P��1cm/s���ٶ���A��D�˶�����Q��2cm/s���ٶ���C��B�˶����ʼ����ֱ��PQ���ı���ABCD�س�һ��ƽ���ı��Σ�
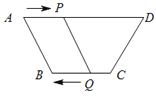
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У������ȷ���ǣ� ��
A.����2y��3=��6y3
B.����ab2��3=��ab6
C.����a��3�£���a2��=a
D.�� ![]() ����1��22=2
����1��22=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD=2AB��F��AD���е㣬��CE��AB������E���߶�AB�ϣ�E����A��B�غϣ�������EF��CF�������н�����һ���������� ( )
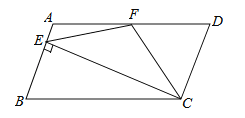
�١�DCF=![]() ��BCD����EF=CF����
��BCD����EF=CF����![]() ���ܡ�DFE=4��AEF��
���ܡ�DFE=4��AEF��
A. �٢ڢۢ� B. �٢ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ž���ֽƬ������ͼ����������ABE��BE���ۣ�ʹ��A���ڶԽ���BD�ϵ�M�㣬����CDF��DF���ۣ�ʹ��C���ڶԽ���BD�ϵ�N�㣮
��1����֤���ı���BFDE��ƽ���ı���.
��2�����ı���BFDE�����Σ�BE =2��������BFDE�������
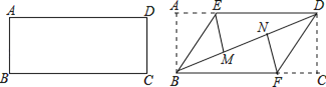
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϫˮ��ľ���ˮλ��![]() ����������Ϫˮ����������·�ij�ܼ���ˮλ�仯���������ĩǡ�ôﵽ����ˮλ��������ʾ��ǰһ��ˮλ�ߣ�������ʾ��ǰһ��ˮλ�ͣ���
����������Ϫˮ����������·�ij�ܼ���ˮλ�仯���������ĩǡ�ôﵽ����ˮλ��������ʾ��ǰһ��ˮλ�ߣ�������ʾ��ǰһ��ˮλ�ͣ���
���� | һ | �� | �� | �� | �� | �� | �� |
ˮλ�仯 |
|
|
|
|
|
|
|

![]() �����ĵ�ˮλ�Ƕ��٣�
�����ĵ�ˮλ�Ƕ��٣�
![]() ������һ�����������ˮλ����ߵģ�
������һ�����������ˮλ����ߵģ�
![]() �Ծ���ˮλΪ��㣬������ͼ����ʾ����ˮλ�����
�Ծ���ˮλΪ��㣬������ͼ����ʾ����ˮλ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѲ����Ħ�г���һ���ϱ������Ѳ�ߣ�ij�����Ӹ�ͤ����������ͣ����![]() �����涨����Ϊ����������ʻ��¼���£���λ��ǧ�ף�
�����涨����Ϊ����������ʻ��¼���£���λ��ǧ�ף�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]() �ڸ�ͤ�η������ͤ��Զ��
�ڸ�ͤ�η������ͤ��Զ��
![]() ����ʻ�����У���Զ����������ж�Զ��
����ʻ�����У���Զ����������ж�Զ��
![]() ��Ħ�г���ʻ
��Ħ�г���ʻ![]() ǧ����
ǧ����![]() ������һ�칲���Ͷ�������
������һ�칲���Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���BAD��ƽ���߽�BC�ڵ�E����ABC��ƽ���߽�AD�ڵ�F��AE��BF�ཻ�ڵ�O������EF

��1����֤���ı���ABEF�����Σ�
��2����AE��6��BF��8��CE��![]() ������ABCD�������
������ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͼ��ÿ��̨���϶�����һ���������µ��ϵĵ�1������4��̨�������α���-5��-2��1��9�������������ĸ�̨�������ĺͶ����.
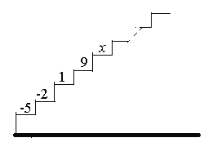
��1����ǰ4��̨�������ĺ��Ƕ��٣�
��2�����5��̨���ϵ���![]() �Ƕ�����
�Ƕ�����
��3�����µ���ǰ���ٸ�̨�������ĺ�Ϊ30.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com