
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣4表示的点与数 _________ 表示的点重合;
(2)若﹣1表示的点与5表示的点重合,回答以下问题:
①13表示的点与数 _________ 表示的点重合;
②若数轴上A、B两点之间的距离为2018(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
![]()
【答案】(1)4;(2)①-9;②A=-1007,B=1011.
【解析】
(1)根据1表示的点与﹣1表示的点重合得出对称中心即可得;
(2)由表示﹣1的点与表示5的点重合,可确定对称点是表示2的点,则:
①表示13的点与对称点距离为11,和左侧表示-9的点重合;
②由题意可得:A、B两点距离对称点的距离为1009,据此求解.
(1)∵1表示的点与﹣1表示的点重合,∴对称中心是原点,∴﹣4表示的点与4表示的点重合.
故答案为:4;
(2)①∵若﹣1表示的点与5表示的点重合,∴对称中心是2表示的点,∵(13-9)÷2=2,∴13表示的点与数﹣9表示的点重合;
②由题意可得:A、B两点距离对称点的距离为2018÷2=1009.
∵对称点是表示2的点,∴A点表示的数是2-1009=-1007,B点表示的数是2+1009=1011.
故答案为:﹣9.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: 
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为(0,1),且过点(﹣1, ![]() ),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
附:阅读材料
任何一个一元二次方程的根与系数的关系为:两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.
即:设一元二次方程ax2+bx+c=0的两根为x1 , x2 ,
则:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
能灵活运用这种关系,有时可以使解题更为简单.
例:不解方程,求方程x2﹣3x=15两根的和与积.
解:原方程变为:x2﹣3x﹣15=0
∵一元二次方程的根与系数有关系:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
∴原方程两根之和=﹣ ![]() =3,两根之积=
=3,两根之积= ![]() =﹣15.
=﹣15.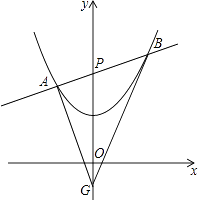
(1)求该二次函数的解析式.
(2)对(1)中的二次函数,当自变量x取值范围在﹣1<x<3时,请写出其函数值y的取值范围;(不必说明理由)
(3)求证:在此二次函数图象下方的y轴上,必存在定点G,使△ABG的内切圆的圆心落在y轴上,并求△GAB面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D. 
(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念学习
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,例如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把![]() (a≠0)记作
(a≠0)记作![]() a
a![]() ,读作“a的圈n次方”.
,读作“a的圈n次方”.
初步探究
(1)直接写出计算结果:2③=________,![]() =________;
=________;
(2)关于除方,下列说法错误的是________
A.任何非零数的圈2次方都等于1; B.对于任何正整数n,1![]() =1;
=1;
C.3④=4③ ; D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
(﹣3)④=________;5⑥=________;![]() =________.
=________.
(2)想一想:将一个非零有理数a的圈n次方写成幂的形式等于________;
(3)算一算:24÷23+(-16)×2④.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是(把你认为正确结论的序号都填上.) 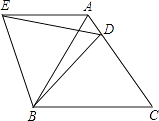
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC. 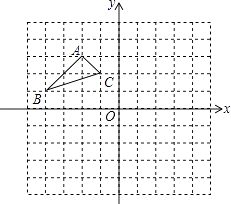
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1 , (只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2 , (只画出图形),写出B2和C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 . 
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在纸面上有一数轴,按要求折叠纸面:
(1)若折叠后数1对应的点与数﹣1对应的点重合,则此时数﹣3对应的点与数 对应的点重合;
(2)若折叠后数2对应的点与数﹣4对应的点重合,则此时数0对应的点与数对 应的点重合;若这样折叠后,数轴上有A、B两点也重合,且A、B两点之间的距离为11(点B在A点的右侧),则点A对应的数为 ,点B对应的数为 .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com