
����Ŀ����֪���κ���ͼ��Ķ�������Ϊ��0��1�����ҹ��㣨��1�� ![]() ����ֱ��y=kx+2��y���ཻ�ڵ�P������κ���ͼ���ڲ�ͬ������A��x1 �� y1����B��x2 �� y2���� ��ע���ڽ�������У���Ҳ�����Ķ�����IJ��ϣ�
����ֱ��y=kx+2��y���ཻ�ڵ�P������κ���ͼ���ڲ�ͬ������A��x1 �� y1����B��x2 �� y2���� ��ע���ڽ�������У���Ҳ�����Ķ�����IJ��ϣ�
�����Ķ�����
�κ�һ��һԪ���η��̵ĸ���ϵ���Ĺ�ϵΪ�������ĺ͵���һ����ϵ���������ϵ���ıȵ��෴���������Ļ����ڳ������������ϵ���ıȣ�
������һԪ���η���ax2+bx+c=0������Ϊx1 �� x2 ��
��x1+x2=�� ![]() ��x1x2=
��x1x2= ![]()
������������ֹ�ϵ����ʱ����ʹ�����Ϊ��
�������ⷽ�̣���x2��3x=15�����ĺ������
�⣺ԭ���̱�Ϊ��x2��3x��15=0
��һԪ���η��̵ĸ���ϵ���й�ϵ��x1+x2=�� ![]() ��x1x2=
��x1x2= ![]()
��ԭ��������֮��=�� ![]() =3������֮��=
=3������֮��= ![]() =��15��
=��15��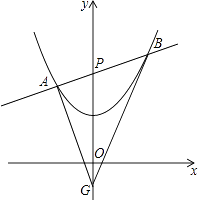
��1����ö��κ����Ľ���ʽ��
��2���ԣ�1���еĶ��κ��������Ա���xȡֵ��Χ�ک�1��x��3ʱ����д���亯��ֵy��ȡֵ��Χ��������˵�����ɣ�
��3����֤���ڴ˶��κ���ͼ���·���y���ϣ��ش��ڶ���G��ʹ��ABG������Բ��Բ������y���ϣ������GAB�������Сֵ��
���𰸡�
��1���⣺���ڶ��κ���ͼ��Ķ�������Ϊ��0��1����
��˶��κ����Ľ���ʽ����Ϊy=ax2+1��
��������y=ax2+1���㣨��1�� ![]() ����
����
�� ![]() =a+1��
=a+1��
��ã�a= ![]() ��
��
����κ����Ľ���ʽΪ��y= ![]() x2+1
x2+1
��2���⣺��x=��1ʱ��y= ![]() ��
��
��x=0ʱ��y=1��
��x=3ʱ��y= ![]() ��32+1=
��32+1= ![]() ��
��
���ͼ1�ɵã�����1��x��3ʱ��y��ȡֵ��Χ��1��y�� ![]()
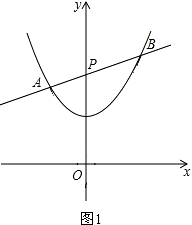
��3����֤��������A��y��ĶԳƵ�A�䣬����BA�䲢�ӳ�����y���ڵ�G������AG����ͼ2��
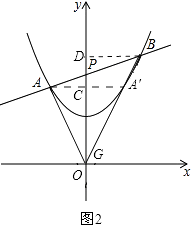
���A������������ϣ��ҡ�AGP=��BGP��
���ABG������Բ��Բ������y���ϣ�
�ߵ�A������Ϊ��x1��y1����
���A�����������x1��y1����
�ߵ�A��x1��y1����B��x2��y2����ֱ��y=kx+2�ϣ�
��y1=kx1+2��y2=kx2+2��
���A�����������x1��kx1+2������B��������x2��kx2+2����
��ֱ��BG�Ľ���ʽΪy=mx+n�����G������Ϊ��0��n����
�ߵ�A�䣨��x1��kx1+2����B��x2��kx2+2����ֱ��BG�ϣ�
�� ![]() ��
��
��ã� 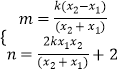 ��
��
��A��x1��y1����B��x2��y2����ֱ��y=kx+2��������y= ![]() x2+1�Ľ��㣬
x2+1�Ľ��㣬
��x1��x2�Ƿ���kx+2= ![]() x2+1��x2��4kx��4=0������ʵ������
x2+1��x2��4kx��4=0������ʵ������
���ɸ���ϵ���Ĺ�ϵ�ɵã�x1+x2=4k��x1x2=��4��
��n= ![]() =��2+2=0��
=��2+2=0��
���G��������0��0����
���ڴ˶��κ���ͼ���·���y���ϣ����ڶ���G��0��0����ʹ��ABG������Բ��Բ������y���ϣ�
�ڽ⣺����A��AC��OP������ΪC������B��BD��OP������ΪD����ͼ2��

��ֱ��y=kx+2��y���ཻ�ڵ�P��
���P��������0��2����
��PG=2��
��S��ABG=S��APG+S��BPG
= ![]() PGAC+
PGAC+ ![]() PGBD
PGBD
= ![]() PG��AC+BD��
PG��AC+BD��
= ![]() ��2������x1+x2��
��2������x1+x2��
=x2��x1
= ![]()
= ![]()
= ![]()
=4 ![]() ��
��
�൱k=0ʱ��S��ABG��С����СֵΪ4��
���GAB�������СֵΪ4��
����������1������κ�������ʽΪy=ax2+1�����ڵ㣨��1�� ![]() ���ڶ��κ���ͼ���ϣ��Ѹõ���������y=ax2+1���������a���Ӷ�������κ����Ľ���ʽ����2���ȷֱ����x=��1��x=0��x=3ʱy��ֵ��Ȼ����ͼ��Ϳɵõ�y��ȡֵ��Χ����3������A��y��ĶԳƵ�A�䣬����BA�䲢�ӳ�����y���ڵ�G������AG����ͼ2�����A������������ϣ��ҡ�AGP=��BGP���ɴ˿ɵá�ABG������Բ��Բ������y���ϣ����ڵ�A��x1 �� y1����B��x2 �� y2����ֱ��y=kx+2�ϣ��Ӷ����Եõ���A������Ϊ��x1 �� kx1+2����A�������Ϊ����x1 �� kx1+2����B������Ϊ��x2 �� kx2+2������ֱ��BG�Ľ���ʽΪy=mx+n�����G������Ϊ��0��n�������ڵ�A�䣨��x1 �� kx1+2����B��x2 �� kx2+2����ֱ��BG�ϣ����ú���k��x1��x2�Ĵ���ʽ��ʾn������A��B��ֱ��y=kx+2��������y=
���ڶ��κ���ͼ���ϣ��Ѹõ���������y=ax2+1���������a���Ӷ�������κ����Ľ���ʽ����2���ȷֱ����x=��1��x=0��x=3ʱy��ֵ��Ȼ����ͼ��Ϳɵõ�y��ȡֵ��Χ����3������A��y��ĶԳƵ�A�䣬����BA�䲢�ӳ�����y���ڵ�G������AG����ͼ2�����A������������ϣ��ҡ�AGP=��BGP���ɴ˿ɵá�ABG������Բ��Բ������y���ϣ����ڵ�A��x1 �� y1����B��x2 �� y2����ֱ��y=kx+2�ϣ��Ӷ����Եõ���A������Ϊ��x1 �� kx1+2����A�������Ϊ����x1 �� kx1+2����B������Ϊ��x2 �� kx2+2������ֱ��BG�Ľ���ʽΪy=mx+n�����G������Ϊ��0��n�������ڵ�A�䣨��x1 �� kx1+2����B��x2 �� kx2+2����ֱ��BG�ϣ����ú���k��x1��x2�Ĵ���ʽ��ʾn������A��B��ֱ��y=kx+2��������y= ![]() x2+1�Ľ��㣬�ɸ���ϵ���Ĺ�ϵ�ɵã�x1+x2=4k��x1x2=��4���Ӷ����n=0������֤�����ڴ˶��κ���ͼ���·���y���ϣ����ڶ���G��0��0����ʹ��ABG������Բ��Բ������y���ϣ���S��ABG=S��APG+S��BPG �� ���Եõ�S��ABG=x2��x1=
x2+1�Ľ��㣬�ɸ���ϵ���Ĺ�ϵ�ɵã�x1+x2=4k��x1x2=��4���Ӷ����n=0������֤�����ڴ˶��κ���ͼ���·���y���ϣ����ڶ���G��0��0����ʹ��ABG������Բ��Բ������y���ϣ���S��ABG=S��APG+S��BPG �� ���Եõ�S��ABG=x2��x1= ![]() =4
=4 ![]() �����Ե�k=0ʱ��S��ABG��С����СֵΪ4��
�����Ե�k=0ʱ��S��ABG��С����СֵΪ4��
�����㾫�����������⣬������Ҫ�˽����ϵ���Ĺ�ϵ(һԪ���η���ax2+bx+c=0��a��0���ĸ��ɷ��̵�ϵ��a��b��c����������֮�͵��ڷ��̵�һ����ϵ�����Զ�����ϵ�����õ��̵��෴��������֮�����ڳ�������Զ�����ϵ�����õ���)����Ҫ����ȷ��һ�κ����ı���ʽ(ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ����)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����л�������·��ͨ�����������涨:С�����ڳ��нֵ�����ʻ�ٶȲ��ó���70 km/h.��ͼ,һ��С������һ�����н�·��ֱ����ʻ,ijһʱ�̸պ���ʻ��·���泵�ټ������ǰ��30 m��,����2 s��,���С�����복�ټ���Ǽ����Ϊ50 m,����С������������?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⣺
���ں�����y=-2x-1��y=3x��y=![]() ��y=-
��y=-![]() ��y=
��y=![]() ��x��0����y��x�����������3��������
��x��0����y��x�����������3��������
���Խ����ഹֱƽ������ȵ��ı����������Σ�
������������ͼ�����������ӽ�����������ߣ���ֻ�����ĶԳ�ͼ�Σ�
����֪����x1��x2��x3�ķ���Ϊs2��������x1+2��x3+2��x3+2�ķ���Ϊs3+2��
������������ĸ����ǣ� ��
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������չÿ�����1Сʱ�����ʦ�Ա�У���꼶ѧ������һ�����������ԣ�����������������ͳ�ƣ������˰�(1)��һ��������������Ƶ���ֲ�ֱ��ͼ�Ͱ��꼶����༶һ������������������ͳ��ͼ.��֪��ͼ1�У�����ֵΪ150��һ��� Ƶ��Ϊ0.2.��˵��: ����ֵΪ190�ε����Ϊ 180��������200��
����ͳ��ͼ����������⣺

��1����(1)��������� ������ֵΪ110��һ���Ƶ��Ϊ ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�����һ������������������120�ε�ͬѧ��Ϊ��꣬���꼶ͬѧһ���������Ĵ���ʲ�����90������ô���꼶ͬѧ�����ж����ˣ���д�������̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC��,��C=90��,BC=6,AC=8,��D���߶�AC�ϴ�C��A�˶�.����CD=x,��ABD�����Ϊy.
(1)��д��y��x֮��Ĺ�ϵʽ.
(2)��xΪ��ֵʱ,y�����ֵ,���ֵ�Ƕ���?��ʱ��D��ʲôλ��?
(3)����ABD���������ABC�������һ��ʱ,��D��ʲôλ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλ����˶�Ա��10�����ѵ���У����аеĻ�����ͼ�� �������ͼ��������������⣺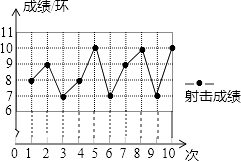
��1�������������ɼ���������д��
������ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ�/�� | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
��2������˶�Ա��10�����ѵ����ƽ���ɼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϣ���˳���Сʯ����ɳ̲�ϰڳɸ�����״���о���.������ͼ1��2�������о���ͼ1�е�1��3��6��10������������Щ���ܹ���ʾ�������Σ������Ϊ�������������Ƶģ���ͼ2�е�1��4��9��16������������Ϊ��������.�������м��������������������������ǣ� ��

A. 289 B. 1225 C. 1024 D. 1378
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֽ������һ���ᣨ��ͼ�����۵�ֽ�森
��1����1��ʾ�ĵ��멁1��ʾ�ĵ��غϣ���4��ʾ�ĵ����� _________ ��ʾ�ĵ��غϣ�
��2������1��ʾ�ĵ���5��ʾ�ĵ��غϣ��ش��������⣺
��13��ʾ�ĵ����� _________ ��ʾ�ĵ��غϣ�
����������A��B����֮��ľ���Ϊ2018��A��B����ࣩ����A��B���㾭�۵����غϣ���A��B�����ʾ�����Ƕ��٣�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬����A������Ϊ����3��0������y�ύ�ڵ�C����D����2����3�����������ϣ� 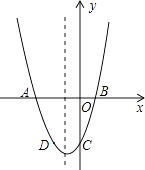
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ�������һ����P�����PA+PD����Сֵ��
��3��������������һ����P��ʹ������ABP�����Ϊ6����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com