
【题目】一位射击运动员在10次射击训练中,命中靶的环数如图. 请你根据图表,完成下列问题: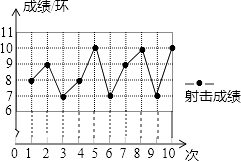
(1)补充完成下面成绩表单的填写:
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.
【答案】
(1)8;9;7
(2)解:运动员这10次射击训练的平均成绩:(8+9+7+8+10+7+9+10+7+10)÷10=8.5(环)
【解析】解:(1)由折线统计图得出第一次射击环数为:8,第二次射击环数为:9,第三次射击环数为:7,所以答案是:8,9,7.
【考点精析】解答此题的关键在于理解统计表的相关知识,掌握制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间,以及对折线统计图的理解,了解能清楚地反映事物的变化情况,但是不能清楚地表示出在总体中所占的百分比.


科目:初中数学 来源: 题型:
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的月历,用带阴影的方框任意框九个数。
(1)图中带阴影的方框中的9个数之和与方框正中心的数有什么关系?请说明你的理由?
(2)若这9个数之和是81,你能说出这9个日期吗?只要回答能或不能,且说明为什么?
(3)这9个数之和可能会是100吗?如果可能,请计算出这9个日期,如果不可能,请说明为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到章丘某旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )

A. 景点离小明家180千米 B. 小明到家的时间为17点
C. 返程的速度为60千米每小时 D. 10点至14点,汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为(0,1),且过点(﹣1, ![]() ),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
附:阅读材料
任何一个一元二次方程的根与系数的关系为:两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.
即:设一元二次方程ax2+bx+c=0的两根为x1 , x2 ,
则:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
能灵活运用这种关系,有时可以使解题更为简单.
例:不解方程,求方程x2﹣3x=15两根的和与积.
解:原方程变为:x2﹣3x﹣15=0
∵一元二次方程的根与系数有关系:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
∴原方程两根之和=﹣ ![]() =3,两根之积=
=3,两根之积= ![]() =﹣15.
=﹣15.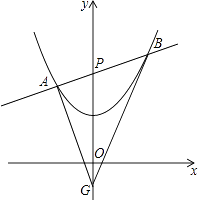
(1)求该二次函数的解析式.
(2)对(1)中的二次函数,当自变量x取值范围在﹣1<x<3时,请写出其函数值y的取值范围;(不必说明理由)
(3)求证:在此二次函数图象下方的y轴上,必存在定点G,使△ABG的内切圆的圆心落在y轴上,并求△GAB面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.在数轴上若点A、B分别表示有理数a、b ,在数轴上A、B两点之间的距离AB=| a-b | .结合数轴与绝对值的知识回答下列问题:
![]()
(1)数轴上表示﹣3和2的两点之间的距离是_____;数轴上表示 x 和 -3 两点之间的距离是_____;
(2)若a表示一个有理数,则|a+4|+|a﹣2|有最小值吗?若有,请求出最小值;若没有,请说明理由;
(3)当a =_____时,|a+4|+|a﹣1|+|a﹣2|的值最小,最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D. 
(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是(把你认为正确结论的序号都填上.) 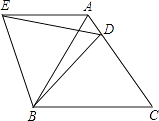
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m为何值时,关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0.
(1)有两个不相等的实数根;
(2)有两个相等的实数根;
(3)没有实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com