
【题目】当m为何值时,关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0.
(1)有两个不相等的实数根;
(2)有两个相等的实数根;
(3)没有实数根.
【答案】
(1)解:(2m+1)x2+4mx+2m﹣3=0,
△=(4m)2﹣4(2m+1)(2m﹣3)=16m+12,
2m+1≠0时,m≠﹣ ![]()
当△>0时,有两个不相等的实数根,即当m>﹣ ![]() 且m≠﹣
且m≠﹣ ![]() 时,方程有两个不相等的实数根
时,方程有两个不相等的实数根
(2)解:当△=0时,有两个不相等的实数根,即当m=﹣ ![]() 时,方程有两个相等的实数根
时,方程有两个相等的实数根
(3)解:当△<0时,没有实数根,即当m<﹣ ![]() 时,方程没有实数根
时,方程没有实数根
【解析】先求出△的值,再根据根的判别式的内容判断即可.
【考点精析】掌握求根公式是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


科目:初中数学 来源: 题型:
【题目】一位射击运动员在10次射击训练中,命中靶的环数如图. 请你根据图表,完成下列问题: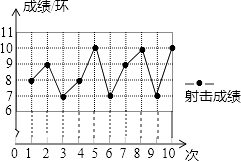
(1)补充完成下面成绩表单的填写:
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数图象如图所示,根据图象可得: 
(1)抛物线顶点坐标;
(2)对称轴为
(3)当x=时,y有最大值是;
(4)当时,y随着x得增大而增大.
(5)当时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上. 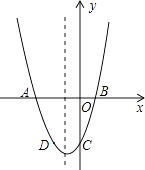
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,左面的几何体叫三棱柱,它有五个面,![]() 条棱,
条棱,![]() 个顶点,中间和右边的几何体分别是四棱柱和五棱柱.
个顶点,中间和右边的几何体分别是四棱柱和五棱柱.

![]() 四棱柱有________个顶点,________条棱,________个面;
四棱柱有________个顶点,________条棱,________个面;
![]() 五棱柱有________个顶点,________条棱,________个面;
五棱柱有________个顶点,________条棱,________个面;
![]() 你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
![]() 棱柱有几个顶点,几条棱,几个面吗?
棱柱有几个顶点,几条棱,几个面吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣12+15﹣|﹣7﹣8|
(2)(﹣3)×(﹣9)﹣(﹣5)
(3)![]()
(4)![]()
化简:(5)![]()
(6)7a+3(a-3b)-2(b-3a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
①四边形ABCD是菱形;
②四边形ABCD是中心对称图形;
③四边形ABCD是轴对称图形;
④AC=BD.
其中正确的是(写上正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( ) 
A.x=1
B.x=﹣1
C.x1=1,x2=﹣3
D.x1=1,x2=﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com