
【题目】某校积极开展每天锻炼1小时活动,老师对本校八年级学生进行一分钟跳绳测试,并对跳绳次数进行统计,绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中,组中值为150次一组的 频率为0.2.(说明: 组中值为190次的组别为 180≤次数<200)
请结合统计图完成下列问题:

(1)八(1)班的人数是 ,组中值为110次一组的频率为 ;
(2)请把频数分布直方图补充完整;
(3)如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%,那么八年级同学至少有多少人?请写出解答过程。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段 | 销售数量 | 销售收入 (元) | |
A种型号 (台) | B种型号 (台) | ||
第一周 | 3 | 2 | 3960 |
第二周 | 5 | 4 | 7120 |
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: 
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的月历,用带阴影的方框任意框九个数。
(1)图中带阴影的方框中的9个数之和与方框正中心的数有什么关系?请说明你的理由?
(2)若这9个数之和是81,你能说出这9个日期吗?只要回答能或不能,且说明为什么?
(3)这9个数之和可能会是100吗?如果可能,请计算出这9个日期,如果不可能,请说明为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳是炽热巨大的气体星球,正以每秒![]() 万吨的速度失去重量.太阳的直径约为
万吨的速度失去重量.太阳的直径约为![]() 万千米,而地球的半径约为
万千米,而地球的半径约为![]() 千米.请将上述三个数据用科学记数法表示,然后计算:
千米.请将上述三个数据用科学记数法表示,然后计算:
(1)在一年内太阳要失去多少万吨重量?
(2)在太阳的直径上能摆放多少个地球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到章丘某旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )

A. 景点离小明家180千米 B. 小明到家的时间为17点
C. 返程的速度为60千米每小时 D. 10点至14点,汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为(0,1),且过点(﹣1, ![]() ),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
附:阅读材料
任何一个一元二次方程的根与系数的关系为:两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.
即:设一元二次方程ax2+bx+c=0的两根为x1 , x2 ,
则:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
能灵活运用这种关系,有时可以使解题更为简单.
例:不解方程,求方程x2﹣3x=15两根的和与积.
解:原方程变为:x2﹣3x﹣15=0
∵一元二次方程的根与系数有关系:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
∴原方程两根之和=﹣ ![]() =3,两根之积=
=3,两根之积= ![]() =﹣15.
=﹣15.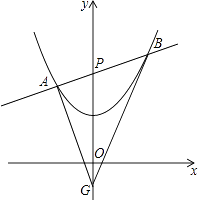
(1)求该二次函数的解析式.
(2)对(1)中的二次函数,当自变量x取值范围在﹣1<x<3时,请写出其函数值y的取值范围;(不必说明理由)
(3)求证:在此二次函数图象下方的y轴上,必存在定点G,使△ABG的内切圆的圆心落在y轴上,并求△GAB面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D. 
(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 . 
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com