
【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段 | 销售数量 | 销售收入 (元) | |
A种型号 (台) | B种型号 (台) | ||
第一周 | 3 | 2 | 3960 |
第二周 | 5 | 4 | 7120 |
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?
【答案】(1) A,B 两种型号的空气净化器的销售单价分别为800元、780元;(2) A型净化器10台、B型净化器20台.
【解析】分析:(1)(1)设A,B 两种型号的空气净化器的销售分别x、y元,根据表格中的两个等量关系列出方程组,解方程组即可求得A,B 两种型号的空气净化器的销售单价;(2)根据题意用x表示出A型净化器的总利润和B型净化器的总利润,即可得 y关于x的函数关系式;(3)根据题意求得x的取值范围,根据一次函数的增减性即可求得销售的最大利润.
详解:
(1)设A,B 两种型号的空气净化器的销售分别x、y元,
根据题意得:
![]() , 解得
, 解得![]() ;
;
即A,B 两种型号的空气净化器的销售单价分别为800元、780元.
(2)①根据题意:A 种型号的空气净化器销售利润为每台200元,共200x元,B种型号的空气净化器销售利润为每台220元,共220(30-x),所以两种型号的净化器利润为:y=200x+220(30-x),即y=-20x+6600.
②由题意得 30-x≤2x, 解得![]() ≥10.
≥10.
∵y=-20x+6600中,-20<0,∴y随x的增大而减小.
∴当x=10时,y取得最大值,此时30-x=20.
答:该商店购进A型净化器10台、B型净化器20台,才能使销售总利润最大


科目:初中数学 来源: 题型:
【题目】甲、乙两个水桶中装有少量且重量相等的水,先把甲桶的水倒出三分之一给乙桶,再把乙桶的水倒出四分之一给甲桶(假设不会溢出),最后甲、乙两桶中水的重量的大小是( )
A. 甲桶中水的重量>乙桶中水的重量 B. 甲桶中水的重量=乙桶中水的重量
C. 甲桶中水的重量<乙桶中水的重量 D. 不能确定,与桶中原有水的重量有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1经过点E(1,0)和F(5,0),并交y轴于D(0,﹣5);抛物线l2:y=ax2﹣(2a+2)x+3(a≠0),
(1)试求抛物线l1的函数解析式;
(2)求证:抛物线 l2与x轴一定有两个不同的交点;
(3)若a=1,抛物线l1、l2顶点分别为、;当x的取值范围是时,抛物线l1、l2 上的点的纵坐标同时随横坐标增大而增大;
(4)若a=1,已知直线MN分别与x轴、l1、l2分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)-23-6×(-3) (2)(+4.3)-|-4|+(-2.3)-(+4)×0
(3)![]() ×2+(-2)3÷|-4| (4)
×2+(-2)3÷|-4| (4)![]() +(
+(![]() )×(-18)
)×(-18)
查看答案和解析>>
科目:初中数学 来源: 题型:
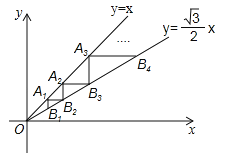
【题目】(2017辽宁省盘锦市,第18题,3分)如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线![]() 于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线
于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线![]() 于点B3,…,按照此规律进行下去,则点An的横坐标为______.
于点B3,…,按照此规律进行下去,则点An的横坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论: ①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )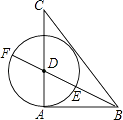
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)、图(c)中,分别画出符合要求(1),(2),(3)的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.



(1)画一个底边为4,面积为8的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个面积为12的平行四边形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展每天锻炼1小时活动,老师对本校八年级学生进行一分钟跳绳测试,并对跳绳次数进行统计,绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中,组中值为150次一组的 频率为0.2.(说明: 组中值为190次的组别为 180≤次数<200)
请结合统计图完成下列问题:

(1)八(1)班的人数是 ,组中值为110次一组的频率为 ;
(2)请把频数分布直方图补充完整;
(3)如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%,那么八年级同学至少有多少人?请写出解答过程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com