
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

【答案】由题意得AC="30m " AB=50m
∵∠ACB=90°
∴BC=![]()
∴小车行驶速度为40÷2=20米/秒
即为20×3600=72千米/小时
∵72千米/小时>70千米/小时
∴这辆小车超速了。
【解析】
(1)由题意知,△ABC为直角三角形,且AB是斜边,已知AB,AC根据勾股定理可以求BC;
(2)根据BC的长度和时间可以求小汽车在BC路程中的速度,若速度大于70千米/时,则小汽车超速;若速度小于70千米/时,则小汽车没有超速.
解:(1)由题意知,AB=130米,AC=50米,
且在Rt△ABC中,AB是斜边,
根据勾股定理AB2=BC2+AC2,
可以求得:BC=120米=0.12千米,
(2)∵6秒=![]() 小时,
小时,
∴速度为![]() =72千米/小时,
=72千米/小时,
故该小汽车超速.
答:该小汽车超速了,平均速度大于70千米/小时.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论: ①a<0,②b<0,③b2﹣4ac>0,④AE+CD=4
下列选项中选出的结论完全正确的是( )
A.①②③
B.①②④
C.①③④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段 | 销售数量 | 销售收入 (元) | |
A种型号 (台) | B种型号 (台) | ||
第一周 | 3 | 2 | 3960 |
第二周 | 5 | 4 | 7120 |
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )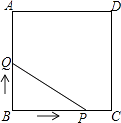
A.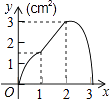
B.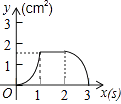
C.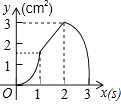
D.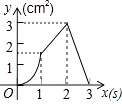
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时)。
(1)用有序实数对表示图中各点。
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: 
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为(0,1),且过点(﹣1, ![]() ),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1 , y1),B(x2 , y2). (注:在解题过程中,你也可以阅读后面的材料)
附:阅读材料
任何一个一元二次方程的根与系数的关系为:两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.
即:设一元二次方程ax2+bx+c=0的两根为x1 , x2 ,
则:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
能灵活运用这种关系,有时可以使解题更为简单.
例:不解方程,求方程x2﹣3x=15两根的和与积.
解:原方程变为:x2﹣3x﹣15=0
∵一元二次方程的根与系数有关系:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
∴原方程两根之和=﹣ ![]() =3,两根之积=
=3,两根之积= ![]() =﹣15.
=﹣15.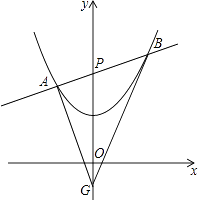
(1)求该二次函数的解析式.
(2)对(1)中的二次函数,当自变量x取值范围在﹣1<x<3时,请写出其函数值y的取值范围;(不必说明理由)
(3)求证:在此二次函数图象下方的y轴上,必存在定点G,使△ABG的内切圆的圆心落在y轴上,并求△GAB面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com