
【题目】如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论: ①a<0,②b<0,③b2﹣4ac>0,④AE+CD=4
下列选项中选出的结论完全正确的是( )
A.①②③
B.①②④
C.①③④
D.①②
【答案】C
【解析】解:①∵抛物线开口向下, ∴a<0,①成立;
②∵抛物线的对称轴为x=﹣ ![]() >0,
>0,
∴b>0,②不成立;
③∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,③成立;
④∵DE为抛物线的对称轴,
∴AE=BE.
∵B点坐标为(4,0),
∴OB=OE+BE=CD+AE=4,④成立.
故选C.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个水桶中装有少量且重量相等的水,先把甲桶的水倒出三分之一给乙桶,再把乙桶的水倒出四分之一给甲桶(假设不会溢出),最后甲、乙两桶中水的重量的大小是( )
A. 甲桶中水的重量>乙桶中水的重量 B. 甲桶中水的重量=乙桶中水的重量
C. 甲桶中水的重量<乙桶中水的重量 D. 不能确定,与桶中原有水的重量有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论: ①a<0,②b<0,③b2﹣4ac>0,④AE+CD=4
下列选项中选出的结论完全正确的是( )
A.①②③
B.①②④
C.①③④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1经过点E(1,0)和F(5,0),并交y轴于D(0,﹣5);抛物线l2:y=ax2﹣(2a+2)x+3(a≠0),
(1)试求抛物线l1的函数解析式;
(2)求证:抛物线 l2与x轴一定有两个不同的交点;
(3)若a=1,抛物线l1、l2顶点分别为、;当x的取值范围是时,抛物线l1、l2 上的点的纵坐标同时随横坐标增大而增大;
(4)若a=1,已知直线MN分别与x轴、l1、l2分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
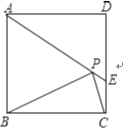
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com