解:(1)△ABC∽△DBA,△CAD∽△AED.
证明如下:∵∠B=∠B,∠ADC=∠BAC,
∴△ABC∽△DBA;
∵∠BAC+∠DAC=∠BAD=∠ADE+∠E,∠DAC=∠E,
∴∠BAC=∠ADE=∠ADC,
∴△CAD∽△AED;
(2)∵△ABC∽△DBA,
∴
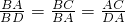
,
∴DA=
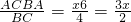
,
∴BD=
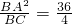
=9.
∴CD=5.
∵△CAD∽△AED,
∴
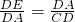
.
∴DE•CD=DA
2,
∴
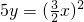
,
∴函数解析式为y=
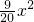
,定义域为2<x<10;
(3)△AED能与△ABC相似.
∵∠BAC=∠ADE=∠ADC,∠BCA>∠ADC=∠ADE,∠BCA>∠CAD=∠E,
∴只有∠B=∠E=∠DAC时,△AED与△ABC相似.
这时,由于∠B+∠BAC+∠CAD+∠ADC=180°,
∴∠BAC+∠DAC=90°,
∴∠ACB=∠BAD=90°,
∴cosB=
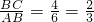
.
分析:(1)△ABC∽△DBA,△CAD∽△AED,由∠B=∠B,∠ADC=∠BAC可以证明△ABC∽△DBA;而∠BAC+∠DAC=∠BAD=∠ADE+∠E,由此得到∠DAC=∠E,这样就∠BAC=∠ADE=∠ADC可以证明△CAD∽△AED;
(2)首先由△ABC∽△DBA可以得到
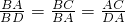
,从而可以用x表示DA,并且求出BD,CD=5,由△CAD∽△AED,得到
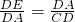
,即DE•CD=DA
2,由此得到
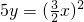
,这样求出函数解析式,然后也可以求出定义域;
(3)△AED能与△ABC相似.首先利用已知条件讨论相似的情况,得到只有△AED与△ABC相似,然后利用相似三角形的性质和已知条件得到这时∠ACB=∠BAD=90°,最后利用三角函数的定义即可求解.
点评:此题既考查了相似三角形的性质与判定,也考查了三角函数的定义,同时也考查了求函数解析式,综合性比较强,解题的关键是多次利用相似三角形的性质与判定,然后利用三角函数解决问题.

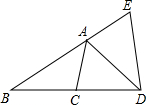 如图,在△ABC中,AB=6,BC=4,点D在边BC的延长线上,∠ADC=∠BAC,点E在边BA的延长线上,∠E=∠DAC.
如图,在△ABC中,AB=6,BC=4,点D在边BC的延长线上,∠ADC=∠BAC,点E在边BA的延长线上,∠E=∠DAC.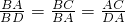 ,
,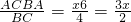 ,
,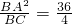 =9.
=9.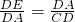 .
.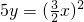 ,
,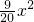 ,定义域为2<x<10;
,定义域为2<x<10;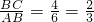 .
.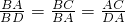 ,从而可以用x表示DA,并且求出BD,CD=5,由△CAD∽△AED,得到
,从而可以用x表示DA,并且求出BD,CD=5,由△CAD∽△AED,得到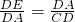 ,即DE•CD=DA2,由此得到
,即DE•CD=DA2,由此得到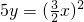 ,这样求出函数解析式,然后也可以求出定义域;
,这样求出函数解析式,然后也可以求出定义域;

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为