
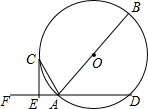
 如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.分析 (1)证明:连接CO,证得∠OCA=∠CAE,由平行线的判定得到OC∥FD,再证得OC⊥CE,即可证得结论;
(2)证明:连接BC,由圆周角定理得到∠BCA=90°,再证得△ABC∽△ACE,根据相似三角形的性质即可证得结论.
解答 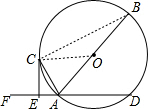 (1)证明:连接CO,
(1)证明:连接CO,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠FAB,
∴∠OCA=∠CAE,
∴OC∥FD,
∵CE⊥DF,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)证明:连接BC,
在Rt△ACE中,AC=$\sqrt{A{E}^{2}+E{C}^{2}}$=$\sqrt{{2}^{2}+{1}^{1}}$=$\sqrt{5}$,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠BCA=∠CEA,
∵∠CAE=∠CAB,
∴△ABC∽△ACE,
∴$\frac{CA}{AB}$=$\frac{AE}{AC}$,
∴$\frac{\sqrt{5}}{AB}=\frac{1}{\sqrt{5}}$,
∴AB=5,
∴AO=2.5,即⊙O的半径为2.5.
点评 本题主要考查了圆周角定理,切线的判定,平行线的性质和判定,勾股定理,相似三角形的判定和性质,熟练掌握切线的判定定理是解决问题的关键.


科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )
如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{3}}{2}$ | C. | $\sqrt{6}$-$\sqrt{3}$ | D. | 2$\sqrt{3}$-$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 矩形ABFE | B. | 矩形EFCD | C. | 矩形EFGH | D. | 矩形DCGH |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 5 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:| 挂果数量x(个) | 频数(株) | 频率 |
| 25≤x<35 | 6 | 0.1 |
| 35≤x<45 | 12 | 0.2 |
| 45≤x<55 | a | 0.25 |
| 55≤x<65 | 18 | b |
| 65≤x<75 | 9 | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 次数 | 2 | 3 | 4 | 5 |
| 人数 | 2 | 2 | 10 | 6 |
| A. | 3次 | B. | 3.5次 | C. | 4次 | D. | 4.5次 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com