
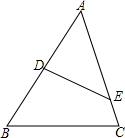
 如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )
如图,在△ABC中,点D、E分别在AB,AC上,则添加下面的条件后△AED与△ABC仍不相似的是( )| A. | $\frac{AD}{AC}$=$\frac{DE}{BC}$ | B. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | C. | ∠AED=∠B | D. | ∠AED=∠C |
科目:初中数学 来源: 题型:选择题
| A. | ∠A+∠C=∠B | B. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | C. | (b+a)(b-a)=c2 | D. | ∠A:∠B:∠C=5:3:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
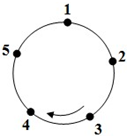 如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
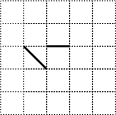 在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )
在如图的正方形网格上画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有( )| A. | 2条 | B. | 3条 | C. | 4条 | D. | 5条 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
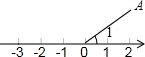 如图,已知线段OA的端点O在原地,∠1=30°,OA=2,在数轴上找一点P,使得△AOP是等腰三角形,并求出点P所表示的数,如果将∠1=30°改为45°或60°,那么点P所表示的数又是多少?
如图,已知线段OA的端点O在原地,∠1=30°,OA=2,在数轴上找一点P,使得△AOP是等腰三角形,并求出点P所表示的数,如果将∠1=30°改为45°或60°,那么点P所表示的数又是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
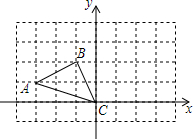 如图所示,在方格纸上建立的平面直角坐标系中:
如图所示,在方格纸上建立的平面直角坐标系中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com