
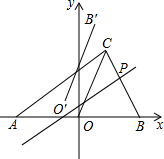
 如图,Rt△ABC的斜边AB在x轴上,OA=OB=6,点C在第一象限,∠A=30°,P(m,n)是线段BC上的动点,过点P作BC的垂线a,以直线a为对称轴,将线段OB轴对称变换后得线段O′B′,
如图,Rt△ABC的斜边AB在x轴上,OA=OB=6,点C在第一象限,∠A=30°,P(m,n)是线段BC上的动点,过点P作BC的垂线a,以直线a为对称轴,将线段OB轴对称变换后得线段O′B′,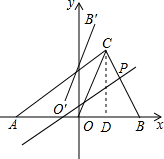 解:(1)过C点作CD⊥AB于点D.
解:(1)过C点作CD⊥AB于点D.| 3 |
| 3 |
| 9 |
| 2 |
3
| ||
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
| 15 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
| 9 |
| 2 |
| 9 |
| 2 |
| 15 |
| 4 |
| 9 |
| 2 |


科目:初中数学 来源: 题型:
 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).查看答案和解析>>
科目:初中数学 来源: 题型:
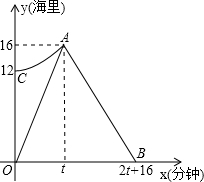 我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的
我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
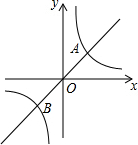 如图,定义:若双曲线y=
如图,定义:若双曲线y=| k |
| x |
| k |
| x |
| 1 |
| x |
| 1 |
| x |
| k |
| x |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com