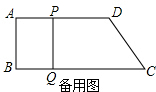
解:(1)∵∠B=90°,AP∥BQ,
∴当AP=BQ时,四边形ABQP成为矩形,
此时有t=22-3t,解得t=

.
∴当t=

s时,四边形ABQP成为矩形;
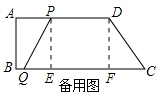
(2)∵PD∥QC,
∴当PQ=CD,PD≠QC时,四边形PQCD为等腰梯形.
过P,D分别作PE⊥BC,DF⊥BC,垂足分别为E,F.
∴四边形ABFD是矩形,四边形PEFD是矩形,
∴BF=AD=16cm,EF=PD,
∵BC=22cm,
∴FC=BC-BF=22-16=6(cm).
由等腰梯形的性质知,QE=FC=6cm.
∴QC=EF+QE+FC=PD+12=AD-AP+12,
即3t=(16-t)+12,解得t=7.
∴当t=7s时,四边形PQCD是等腰梯形;
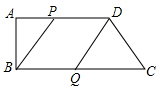
(3)四边形PBQD不能成为菱形.理由如下:
∵PD∥BQ,
∴当PD=BQ=BP时,四边形PBQD能成为菱形.
由PD=BQ,得16-t=22-3t,解得t=3,
当t=3时,PD=BQ=13,BP=

=
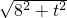
=

=

≠13,
∴四边形PBQD不能成为菱形;
如果Q点的速度改变为vcm/s时,能够使四边形PBQD在时刻ts为菱形,
由题意,得
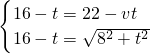
,解得
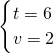
.
故点Q的速度为2cm/s时,能够使四边形PBQD在某一时刻为菱形.
分析:(1)因为∠B=90°,AP∥BQ,由矩形的判定可知当AP=BQ时,四边形ABQP成为矩形;
(2)因为PD∥QC,当PQ=CD,PD≠QC时,四边形PQCD为等腰梯形.过P,D分别作PE⊥BC,DF⊥BC后,可求出CF=6,所以当等腰梯形成立时,CQ=PD+12,然后列方程解答即可;
(3)因为PD∥BQ,当PD=BQ=BP时,四边形PBQD能成为菱形,先由PD=BQ求出运动时间t的值,再代入求BP,发现BP≠PD,判断此时四边形PBQD不能成为菱形;设Q点的速度改变为vcm/s时,四边形PBQD在时刻t为菱形,根据PD=BQ=BP列出关于v、t的方程组,解方程组即可求出点Q的速度.
点评:本题借助动点主要考查了矩形、菱形的判定,勾股定理,等腰梯形的判定与性质,以及方程和方程组在几何图形中的应用,难度适中,用含t的代数式正确表示出相关线段的长度是解题的关键.


 解:(1)∵∠B=90°,AP∥BQ,
解:(1)∵∠B=90°,AP∥BQ, .
. s时,四边形ABQP成为矩形;
s时,四边形ABQP成为矩形; (2)∵PD∥QC,
(2)∵PD∥QC, (3)四边形PBQD不能成为菱形.理由如下:
(3)四边形PBQD不能成为菱形.理由如下: =
=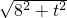 =
= =
= ≠13,
≠13,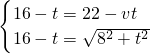 ,解得
,解得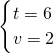 .
.

 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )