
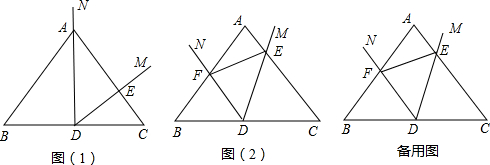
分析 (1)根据等腰三角形的性质以及相似三角形的判定得出相似三角形即可;
(2)利用已知首先求出∠BFD=∠CDE,即可得出△BDF∽△CED,再利用相似三角形的性质得出BD:DF=EC:DE,进而得出△BDF∽△CED∽△DEF.
(3)首先利用△DEF的面积等于△ABC的面积的$\frac{1}{4}$,求出DH的长,进而利用S△DEF的值求出EF即可.
解答 解:(1)图(1)中与△ADE相似的有△ABD,△ACD,△DCE.
理由如下:∵AB=AC,D为BC的中点,
∴AD⊥BC,∠B=∠C,∠BAD=∠CAD,
又∵∠MDN=∠B,
∴△ADE∽△ABD,
同理可得:△ADE∽△ACD,
∵∠MDN=∠C=∠B,
∠B+∠BAD=90°,∠ADE+∠EDC=90°,
∠B=∠MDN,
∴∠BAD=∠EDC,
∵∠B=∠C,
∴△ABD∽△DCE,
∴△ADE∽△DCE,
(2)△BDF∽△CED∽△DEF,
证明:∵∠B+∠BDF+∠BFD=180°
∠EDF+∠BDF+∠CDE=180°,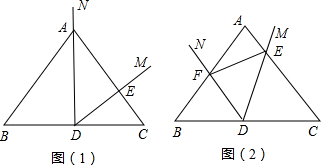
又∵∠EDF=∠B,∴∠BFD=∠CDE,
由AB=AC,得∠B=∠C,
∴△BDF∽△CED,
∴$\frac{BD}{DF}$=$\frac{EC}{DE}$
∵BD=CD,
∴$\frac{CD}{DF}$=$\frac{EC}{DE}$.
又∵∠C=∠EDF,
∴△BDF∽△CED∽△DEF.
(3)连接AD,过D点作DG⊥EF,DH⊥BF,垂足分别为G,H.
∵AB=AC,D是BC的中点,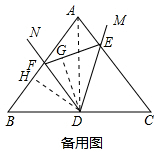
∴AD⊥BC,BD=$\frac{1}{2}$BC=6.
在Rt△ABD中,AD2=AB2-BD2,
∴AD=8,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×12×8=48.
S△DEF=$\frac{1}{4}$S△ABC=$\frac{1}{4}$×48=12.
又∵$\frac{1}{2}$AD•BD=$\frac{1}{2}$AB•DH,
∴DH=$\frac{AD•BD}{AB}$=$\frac{8×6}{10}$=4.8,
∵△BDF∽△DEF,
∴∠DFB=∠EFD
∵DG⊥EF,DH⊥BF,
∴DH=DG=4.8.
∵S△DEF=$\frac{1}{2}$×EF×DG=12,
∴EF=$\frac{12}{\frac{1}{2}DG}$=5.
点评 本题考查了和相似有关的综合性题目,用到的知识点有三角形相似的判定和性质、等腰三角形的性质以及勾股定理的运用,灵活运用相似三角形的判定定理和性质定理是解题的关键,解答时,要仔细观察图形、选择合适的判定方法,注意数形结合思想的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 数据3、5、4、1、-2的中位数是3 | |
| B. | 数据1、1、0、2、4的平均数是2 | |
| C. | 在选举中,人们通常最关心是数据的众数 | |
| D. | 甲乙两人近5次数学考试平均分都是95分,方差分别是2.5和8.5,要选一人参加数学竞赛,选甲比较合适 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
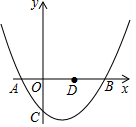 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
| 温度y/℃ | … | -20 | -10 | -8 | -5 | -4 | -8 | -12 | -16 | -20 | -10 | -8 | -5 | -4 | a | -20 | … |
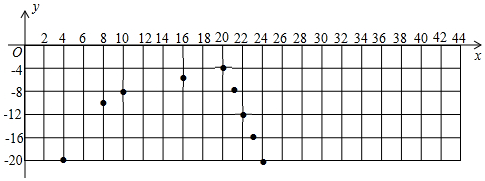
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com