
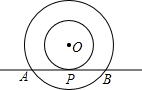
 如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.
如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P. 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:填空题
某商场将一款品牌时装按标价打九折出售,可获利80%,若按标价打七折出售,可获利______%。
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | a2 | C. | -a | D. | $\frac{1}{a^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为1m/s,则这个人运动到点M所用时间是3s.
如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为1m/s,则这个人运动到点M所用时间是3s.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
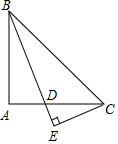 已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.
已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
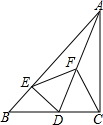 如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.
如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
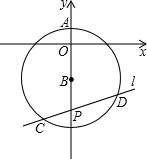 如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,-7)的直线l与⊙B相交于C,D两点,则弦CD长的所有可能的整数值有3个.
如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,-7)的直线l与⊙B相交于C,D两点,则弦CD长的所有可能的整数值有3个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com