练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．设x＜0，若-3xn•x5＞0，则n为偶数（奇或偶）．

    分析 由-3xn•x5＞0知-3xn+5＞0，可得xn+5＜0，结合x＜0知n+5为奇数，则n为偶数．

    解答 解：∵-3xn•x5＞0，
    ∴-3xn+5＞0，
    ∴xn+5＜0，
    又∵x＜0，
    ∴n+5为奇数，
    则n为偶数，
    故答案为：偶．

    点评 本题主要考查单项式乘以单项式及乘方的运算法则，根据熟练掌握单项式乘以单项式的运算法则和乘方的运算法则是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年北京市西城区七年级上学期期末考试数学试卷（解析版） 题型：解答题

    13+（-5）-（-21）-19

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，以点O为圆心的两个同心圆中，大圆的弦AB切小圆于点P．
    （1）PA与PB相等吗？请说明理由；
    （2）若AB=8，求圆环的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．①如图1：A、B是两个蓄水池，都在河流a的同侧，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A、B两地，问该站建在河边什么地方，可使所修的渠道最短，试在图中确定该点的位置（保留作图痕迹）．
    ②如图2：某地有两个工厂M、N和两条相交叉的公路a，b现计划修建一座物资仓库，希望仓库到两个工厂的距离相等，到两条公路的距离也相等．你能确定仓库应该建在什么位置吗？在所给的图形中画出你的设计方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．△ABC的边BC在直线l上，点D、E是直线l的两点，且BA=BD，CA=CE．
    （1）如图1，若AB=AC，∠BAC=90°，求∠DAE的度数；
    （2）如图2，若∠BAC=90°，求∠DAE的度数；
    （3）如图3，设∠BAC=ɑ，∠DAE=β，请写出ɑ，β之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．将一副直角三角板按图1放置，∠ACB=∠CDE=90°，AB边交直线DE于点M，∠CAB=60°，∠ABC=30°，∠ECD=45°，设∠BMD=α，∠BCE=β．
    （1）如图1，猜想α和β之间的关系，并证明你的猜想；
    （2）当其中一个三角板旋转时，如图2，直接写出α和β之间的关系：α+β=165°；
    （3）如图3，作∠AME的角平分线交CE于点F，当β=14°，求∠CFM的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．一辆汽车在公路上行驶，其所走的路程和所用的时间可用下表表示：
    时间/t（min）12.55102050…
    路程/s（km）25102040100…
    （1）在这个变化过程中，自变量、因变量各是什么？
    （2）当汽车行驶路程s为20km时，所花的时间t是多少分钟？
    （3）从表中说出随着t逐渐变大，s的变化趋势是什么？
    （4）如果汽车行驶的时间为t（min），行驶的路程为s（km），那么路程s与时间t之间的关系式为s=2t．
    （5）按照这一行驶规律，当所花的时间t是300min时，汽车行驶的路程s是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

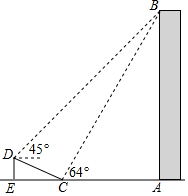    6．如图，在大楼AB的正前方有一斜坡CD长为13米，坡度为1：$\frac{12}{5}$，高为DE．在斜坡底的点C处测得楼顶B的仰角为64°，在斜坡顶的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上，求斜坡的高 DE与大楼AB的高度．（参考数据：sin64°≈0.9，tan64°≈2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．北京时间201611月1日7时，三峡水库水位达到175米，蓄水量39300000000立方米，标志着2016年三峡水库试验性蓄水任务顺利完成，其中39300000000立方米用科学记数法表示为（　　）
    A．0.393×1011立方米B．3.93×1010立方米
    C．0.393×1010立方米D．3.93×1011立方米

    查看答案和解析>>

    同步练习册答案