
【题目】如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为 . 
科目:初中数学 来源: 题型:
【题目】下列各组线段的长度成比例的是( )
A. 6cm、2cm、1cm、4cm B. 4cm、5cm、6cm、7cm
C. 3cm、4cm、5cm、6cm D. 6cm、3cm、8cm、4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,AB=![]() ,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
(1)求证:BE=DF;
(2)当t= 秒时,DF的长度有最小值,最小值等于 ;
(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?
(4)如图3,将线段CD绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CG.在点E的运动过程中,当它的对应点F位于直线AD上方时,直接写出点F到直线AD的距离y关于时间t的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( ) 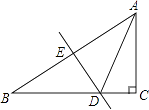
A.6
B.6 ![]()
C.9
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年约5000名初三学生参加数学中考,从中抽取300名考生的数学成绩进行分析,则在该调查中,样本指的是 ( )
A. 300 B. 300名 C. 5000名考生的数学成绩 D. 300名考生的数学成绩
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com