
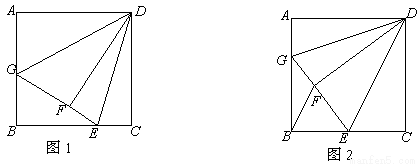
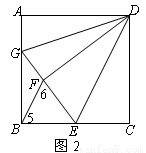
如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.
(1) 求证:∠EDG=45°.
(2) 如图2,E为BC的中点,连接BF.
①求证:BF∥DE;
②若正方形边长为6,求线段AG的长.
(3) 当BE︰EC= 时,DE=DG.
(1)证明见解析;(2)证明见解析,2;(3)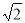 .
.
【解析】
试题分析:(1)易证△DGA≌△DGF,知∠3=∠4,由折叠得∠1=∠2,所以∠EDG=∠3+∠2=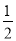 (∠ADF+∠FDC)= 45°;
(∠ADF+∠FDC)= 45°;
(2)如图2由折叠易知∠5=∠6,再由三角形的外角知∠5=∠DEC,得证BF∥DE;由勾股定理可求AG的长;
(3)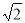 .
.
试题解析:(1)证明:如图:
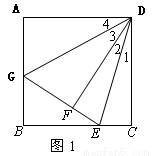
∵四边形ABCD是正方形,
∴DC=DA.∠A=∠B=∠C=∠ADC = 90°.
∵ △DEC沿DE折叠得到△DEF,
∴∠DFE=∠C,DC=DF,∠1=∠2,
∴∠DFG=∠A,DA=DF,
又∵DG=DG,
∴△DGA≌△DGF,
∴∠3=∠4,
∴∠EDG=∠3+∠2=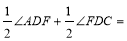
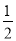 (∠ADF+∠FDC)= 45°.
(∠ADF+∠FDC)= 45°.
(2) ①证明:∵△DEC沿DE折叠得到△DEF,E为BC的中点
∴CE=EF=BE,∠DEF=∠DEC.
∴∠5=∠6,
∵∠FEC=∠5+∠6,∴∠DEF+∠DEC=∠5+∠6
∴2∠5=2∠DEC,即∠5=∠DEC
∴BF∥DE.
②【解析】
设AG=x,则GF=x,BG=6-x,
由正方形边长为6,得CE=EF=BE=3,
∴GE=EF+GF=3+x.
在Rt△GBE中,根据勾股定理得:
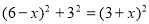
解得x=2,即线段AG的长为2.
(3) 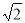 .
.
考点:1.全等三角形的判定与性质;2.平行线的判定;3.勾股定理.


科目:初中数学 来源:2015届江苏省常熟市八年级下学期期末考试数学试卷(解析版) 题型:解答题
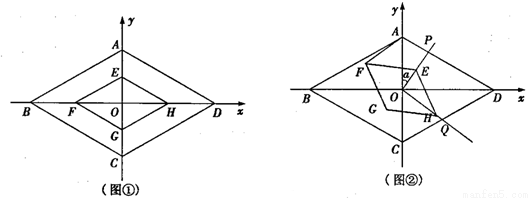
如图①,两个菱形ABCD和EFGH是以坐标原点O为位似中心的位似图形,对角线均在坐标轴上,已知菱形EFGH与菱形ABCD的相似比为1:2,∠BAD=120°,其中AD=4.
(1)点D坐标为 ,点E坐标为 ;
(2)固定图①中的菱形ABCD,将菱形EFCH绕O点顺时针方向旋转α度角(0°<α<90°),并延长OE交AD于P,延长OH交CD于Q,如图②所示,
①当α=30°时,求点P的坐标;
②试探究:在旋转的过程中是否存在某一角度α,使得四边形AFEP是平行四边形?若存在,请推断出α的值;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源:2015届江苏省南京高淳八年级下学期期中检测数学试卷(解析版) 题型:解答题
如图,平行四边形ABCD中,AE⊥BD, CF⊥BD,垂足分别为E、F.求证:四边形AECF是平行四边形.

查看答案和解析>>
科目:初中数学 来源:2015届江苏省南京高淳八年级下学期期中检测数学试卷(解析版) 题型:选择题
一只不透明的袋中装有除颜色外完全相同的6个球,其中3个红球、3个黄球,将球摇匀.从袋中任意摸出3个球,则其中至少有2个球同色的事件是 事件.(填“必然”、“不可能”、“随机”)
查看答案和解析>>
科目:初中数学 来源:2015届江苏省兴化市八年级下学期期中考试数学试卷(解析版) 题型:解答题
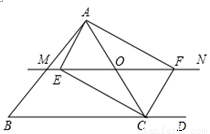
如图,△ABC中,O是AC上的任意一点(不与点A、C重合),过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2015届江苏无锡市八年级下学期期中考试数学卷(解析版) 题型:选择题
如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是
A.BA=BC B.AB//CD C.AC=BD D.AC、BD互相平分

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com