
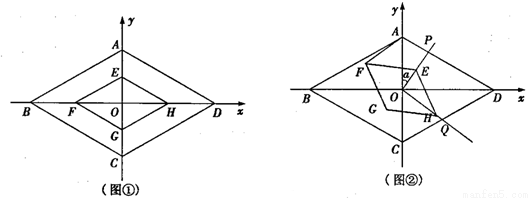
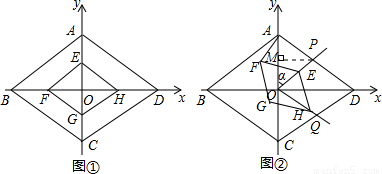
如图①,两个菱形ABCD和EFGH是以坐标原点O为位似中心的位似图形,对角线均在坐标轴上,已知菱形EFGH与菱形ABCD的相似比为1:2,∠BAD=120°,其中AD=4.
(1)点D坐标为 ,点E坐标为 ;
(2)固定图①中的菱形ABCD,将菱形EFCH绕O点顺时针方向旋转α度角(0°<α<90°),并延长OE交AD于P,延长OH交CD于Q,如图②所示,
①当α=30°时,求点P的坐标;
②试探究:在旋转的过程中是否存在某一角度α,使得四边形AFEP是平行四边形?若存在,请推断出α的值;若不存在,说明理由;
(1)点D坐标为(2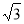 ,0),点E坐标为(0,1).
,0),点E坐标为(0,1).
(2)①点P的坐标是(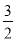 ,
,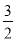 );
);
②当α=60°时,四边形AFEP是平行四边形.理由见解析
【解析】
试题分析:(1)由于∠BAD=120°,易知∠OAD=60°,通过解直角△AOD来求OD、OA的长度;然后利用相似比来求OE的长度;
(2)由(1)和相似多边形的性质知,OA=2,OD=2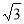 ,EF=2.
,EF=2.
①作PM⊥OA于点M,易求AM、PM的长度;
②如果四边形AFEP是平行四边形,那么首要满足的条件是AP∥FE,由于∠FEO=60°,因此∠APO必为60°,此时△AOP中,∠APO=∠OAP=60°,因此△AOP是等边三角形,已知两菱形的位似比为2:1,因此EF= 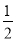 AD,也就是EF=AP,由此可得出当α=60°时,AP //EF,且AP=EF,即四边形APEF是平行四边形.
AD,也就是EF=AP,由此可得出当α=60°时,AP //EF,且AP=EF,即四边形APEF是平行四边形.
试题解析:(1)如图①,∵∠BAD=120°,四边形ABCD是菱形,
∴∠OAD=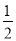 ∠BAD=60°.
∠BAD=60°.
又∵在直角△AOD中,AD=4,
∴OA=AD•cos60°=4×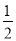 =2,
=2,
OD=AD•sin60°=4×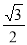 =2
=2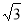 .
.
又菱形EFGH与菱形ABCD的相似比为1:2,
∴OE:OA=1:2,
∴OE=1,
∴点D坐标为(2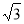 ,0),点E坐标为(0,1).
,0),点E坐标为(0,1).
故答案是:(2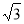 ,0),(0,1);
,0),(0,1);
(2)由(1)知,OA=2,OD=2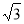 ,∠OAD=60°.
,∠OAD=60°.
∵菱形EFGH与菱形ABCD的相似比为1:2,AD=4,
∴EF=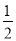 AB=
AB=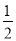 AD=2.
AD=2.
①当α=30°时,∠APO=90°,则AP=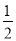 OA=1.
OA=1.
如图②,作PM⊥OA于点M.则AM=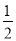 AP=
AP=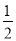 ,PM=
,PM=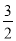 ,
,
∵OM=OA-AM=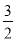 ,
,
∴点P的坐标是( ,
, );
);
②当α=60°时,四边形AFEP是平行四边形.理由如下:
∵在旋转过程中,EF=2,∠FEO=60°,∠OAP=60°,当射线OE旋转角度α=60°时,得△AOP是等边三角形,此时∠APO=60°,AP=2,
∴AP=EF,
∴∠APO=∠FEO,得AP∥EF,
∴四边形AFEP是平行四边形,
∴当α=60°时,四边形AFEP是平行四边形.
考点:1、菱形的性质;2、解直角三角形;3、图形的旋转变换;4、相似多边形的性质


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:2015届江苏省江阴市八年级下学期期中考试数学试卷(解析版) 题型:解答题
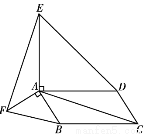
如图,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.
查看答案和解析>>
科目:初中数学 来源:2015届江苏省心校三校八年级下学期第三次联考数学卷(解析版) 题型:选择题
若有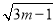 意义,则m能取的最小整数值是( )
意义,则m能取的最小整数值是( )
A.m=0 B.m=1 C.m=2 D.m=3
查看答案和解析>>
科目:初中数学 来源:2015届江苏省无锡市崇安区八年级下学期期中统考数学试卷(解析版) 题型:填空题
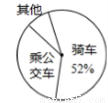
某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知乘公交车上学的学生有20人,骑自行车上学的学生有26人,则乘公交车上学的学生人数在扇形统计图中对应的扇形所占的圆心角的度数为 .
查看答案和解析>>
科目:初中数学 来源:2015届江苏省无锡市崇安区八年级下学期期中统考数学试卷(解析版) 题型:选择题
如图,在□ABCD中,AC与BD相交于点O,则下列结论不一定成立的是…( )
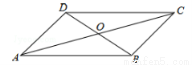
A.BO=DO B.CD=AB C.∠BAD=∠BCD D.AC=BD
查看答案和解析>>
科目:初中数学 来源:2015届江苏省常熟市八年级下学期期末考试数学试卷(解析版) 题型:解答题
如图,在□ABCD中,点E在BC上,∠CDE=∠DAE.
(1)求证:△ADE∽△DEC;
(2)若AD=6,DE=4,求BE的长.

查看答案和解析>>
科目:初中数学 来源:2015届江苏省常熟市八年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,点A、B在反比例函数y=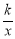 (k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为 .
(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为 .

查看答案和解析>>
科目:初中数学 来源:2015届江苏省南京高淳八年级下学期期中检测数学试卷(解析版) 题型:解答题
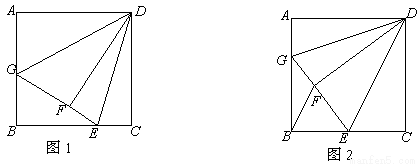
如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.
(1) 求证:∠EDG=45°.
(2) 如图2,E为BC的中点,连接BF.
①求证:BF∥DE;
②若正方形边长为6,求线段AG的长.
(3) 当BE︰EC= 时,DE=DG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com