
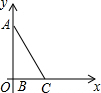
 在Rt△ABC中,∠ABC=90°,AB=4,BC=2.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,点C到原点的最大距离为2+2$\sqrt{2}$.
在Rt△ABC中,∠ABC=90°,AB=4,BC=2.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,点C到原点的最大距离为2+2$\sqrt{2}$. 分析 根据题意首先取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,进而求出答案.
解答  解:如图所示:取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,在
解:如图所示:取A1B1的中点E,连接OE,C1E,当O,E,C1在一条直线上时,点C到原点的距离最大,在
Rt△A1OB1中,∵A1B1=AB=4,点OE为斜边中线,
∴OE=B1E=$\frac{1}{2}$A1B1=2,
又∵B1C1=BC=2,
∴C1E=$\sqrt{{B}_{1}{C}_{1}^{2}+{B}_{1}{E}^{2}}$=2$\sqrt{2}$,
∴点C到原点的最大距离为:OE+C1E=2+2$\sqrt{2}$.
故答案为:2+2$\sqrt{2}$.
点评 此题主要考查了轨迹以及勾股定理等知识,正确得出C点位置是解题关键.


科目:初中数学 来源:2016-2017学年江苏省东台市第四教育联盟八年级下学期第一次月考数学试卷(解析版) 题型:填空题
一个正方形要绕它的中心至少旋转_______度才能与原来的图形重合.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com