解:(1)设点C的坐标为(x,y),
∵A(-4,0)、B(0,4),

=

,
∴
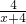
=
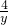
=

=

,
解得x=5,y=9,
∴点C(5,9);
(2)∵B(0,4),
∴设抛物线解析式为y=ax
2+bx+4,
∵C(5,9),
∴25a+5b+4=9,
∴b=1-5a,
∴抛物线解析式为y=ax
2+(1-5a)x+4,
∵△=b
2-4ac=(1-5a)
2-16a=0,
∴25a
2-26a+1=0,
解得a
1=1,a
2=

,
∵x=-

=-
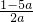
>0,
解得a<0或a>

,
∴a=1,
∴y=x
2-4x+4;
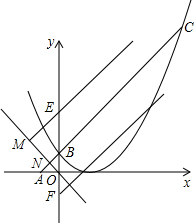
(3)如图,过点O作BC的垂线交BC于点N,设点P所在的直线ME交y轴于点E,交BC的垂线于点M,
则MN=3

,
∵A(-4,0)、B(0,4),
∴AO=4,OB=4,
∴△AOB是等腰直角三角形,
∴ON=AO•sin45°=4×

=2

,
∴OM=ON+MN=2

+3

=5

,
∴

=

=
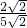
=

,
∴OE=

OB=

×4=10,
∴点E的坐标为(0,10),
∴直线ME的解析式为y=x+10
由
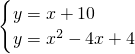
,
解得
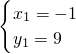
,
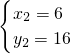
,
同理:点F为(0,-2),
由
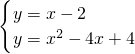
,
解得

,
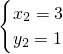
,
∴点P的坐标为(-1,9)或(6,16)或(2,0)或(3,1).
分析:(1)设点C的坐标为(x,y),然后根据位似比列式求出a、b的值,即可得解;
(2)根据点B、C的坐标设出抛物线的解析式,再根据顶点落在x轴的正半轴上可知,抛物线与x轴只有一个交点,所以△=b
2-4ac=0,且x=-

>0,从而求出抛物线的解析式;
(3)过点O作BC的垂线交BC于点N,根据点A、B的坐标可知△AOB是等腰直角三角形,然后求出ON的长度,设点P所在的直线ME交y轴于点E,交BC的垂线于点M,然后根据相似三角形对应边成比例列式求出OE的长度,然后求出直线ME的解析式,与抛物线解析式联立求解即可得到点P的坐标,同理当点E在点B的下方时,求出直线的解析式,与抛物线解析式联立求解得到点P的坐标,从而得解.
点评:本题综合考查了二次函数的问题,待定系数法求函数解析式,抛物线与x轴的交点问题,点到直线的距离,位似变换的性质,等腰直角三角形的性质,函数图象的交点的求解方法,综合性较强,难度较大,根据顶点在x轴的正半轴上求出抛物线的解析式是解题的关键.

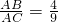 .
. ,求点P的坐标.
,求点P的坐标. =
= ,
,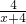 =
=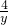 =
= =
= ,
, ,
, =-
=-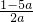 >0,
>0,
 ,
, ,
, =2
=2 ,
, +3
+3 =5
=5 ,
, =
= =
=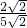 =
= ,
, OB=
OB= ×4=10,
×4=10,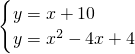 ,
,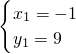 ,
,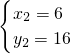 ,
,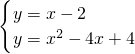 ,
, ,
,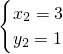 ,
, >0,从而求出抛物线的解析式;
>0,从而求出抛物线的解析式;

 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.