【题目】在直角坐标系中，点P（－3，2）关于x轴对称点的坐标是（ ）
A. （3，2） B. （3，－2） C. （－3，2） D. （－3，－2）
科目：初中数学 来源： 题型：
【题目】某市今年约有140000人报名参加初中学业水平考试，用科学记数法表示140000为（ ）
A.14×104
B.14×103
C.1.4×104
D.1.4×105
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2014年1月，国家发改委出台指导意见，要求2015年底前，所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响，随机访问了自己居住在小区的部分居民，就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查，并把调查结果整理成下面的图1，图2.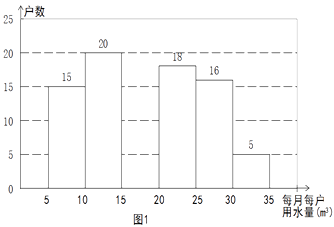
小军发现每月每户的用水量在5m3-35m3之间，有7户居民对用水价格调价涨幅抱无所谓，不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息，完成下列问题：
（1）n = ， 小明调查了户居民，并补全图1；
（2）每月每户用水量的中位数落在之间，众数落在之间；
（3）如果小明所在的小区有1200户居民，请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中，已知抛物线
与
轴交于
，
两点，与
轴交于点
.
(1)求抛物线的函数表达式；
(2)若点
是
轴上的一点，且以
为顶点的三角形与
相似，求点
的坐标；
(3)如图2，
轴玮抛物线相交于点
，点
是直线
下方抛物线上的动点，过点
且与
轴平行的直线与
，
分别交于点
，
，试探究当点
运动到何处时，四边形
的面积最大，求点
的坐标及最大面积；
(4)若点
为抛物线的顶点，点
是该抛物线上的一点，在
轴，
轴上分别找点
，
，使四边形
的周长最小，求出点
，
的坐标.
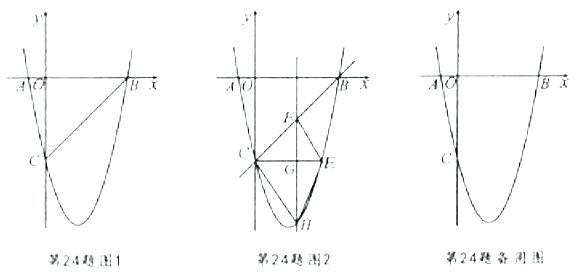
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线的解析式为
.
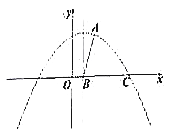
（1）当自变量
时，函数值
随
的增大而减少，求
的取值范围；
（2）如图，若抛物线的图象经过点
，与
轴交于点
，抛物线的对称轴与
轴交于
.
①求抛物线的解析式；
②在抛物线上是否存在点
，使得
？若存在，求出点
的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，动点
在以
为圆心，
为直径的半圆弧上运动（点
不与点
及
的中点
重合），连接
.过点
作
于点
，以
为边在半圆同侧作正方形
，过
点作
的切线交射线
于点
，连接
、
.
（1）探究：如左图，当
动点在
上运动时；
①判断
是否成立？请说明理由；
②设
，
是否为定值？若是，求出该定值，若不是，请说明理由；
③设
，
是否为定值？若是，求出该定值，若不是，请说明理由；
（2）拓展：如右图，当动点
在
上运动时；
分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论.（均不必说明理由）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若△ABC的三边a,b,c满足(ac)(a2+b2c2)=0,则△ABC是( )
A. 等腰三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列各数中，正确的角度互化是（ ）
A.63.5°=63°50′B.23°12′36″=23.48°
C.18°18′18″=18.33°D.22.25°=22°15′
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
