
【题目】如图,动点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为直径的半圆弧上运动(点
为直径的半圆弧上运动(点![]() 不与点
不与点![]() 及
及![]() 的中点
的中点![]() 重合),连接
重合),连接![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为边在半圆同侧作正方形
为边在半圆同侧作正方形![]() ,过
,过![]() 点作
点作![]() 的切线交射线
的切线交射线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
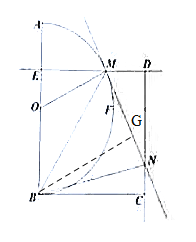
(1)探究:如左图,当![]() 动点在
动点在![]() 上运动时;
上运动时;
①判断![]() 是否成立?请说明理由;
是否成立?请说明理由;
②设![]() ,
,![]() 是否为定值?若是,求出该定值,若不是,请说明理由;
是否为定值?若是,求出该定值,若不是,请说明理由;
③设![]() ,
,![]() 是否为定值?若是,求出该定值,若不是,请说明理由;
是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如右图,当动点![]() 在
在![]() 上运动时;
上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)

【答案】(1)①成立,理由见解析;②为定值1;③![]() 为定值45°;(2)不发生变化.
为定值45°;(2)不发生变化.
【解析】
试题分析:(1) ①∠MEO=∠MDN=90°,∠MOE=∠DMN,证明△OEM∽△MDN;②过点B作BG⊥MN, 证明△BME≌△BMG, 得BM=MG,再证明△BNG≌△BCN,得GN=CN,从而得k=1;③由②知∠OBM=∠MBG得BM=MG, 有△BNG≌△BCN,得∠GBN=∠CBN,,即可得![]() 为定值45°;(2)和(1)的思路相同,不发生变化.
为定值45°;(2)和(1)的思路相同,不发生变化.
试题解析:
(1)①成立,理由如下:
过点M作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,
∴∠MEO=∠MDN=90°,
∴∠MOE+∠EMO=90°
过M点的![]() 的切线交射线DC于点N,
的切线交射线DC于点N,
∴∠OMN=90°,
∴∠DMN+∠EMO=90°
∴∠MOE=∠DMN
∴△OEM∽△MDN
②k是定值1,理由如下:
过点B作BG⊥MN,
∵过M点的![]() 的切线交射线DC于点N,
的切线交射线DC于点N,
∴∠OMN=90°,
∵BG⊥MN,
∴∠BGM=90°,
∴∠OMN=∠BGM=90°,
∴OM∥BG
∴∠OMB=∠MBG,
∵OM=OB
∴∠OMB=∠OBM,
∴∠OBM=∠MBG,
∴△BME≌△BMG,
∴BM=MG,BG=BE,
∵正方形BCDE,
∴BG=BC
∴△BNG≌△BCN,
∴GN=CN
∴MN=MG+NG=ME+CN
即![]()
③![]() 为定值45°,理由如下:
为定值45°,理由如下:
由②知:∠OBM=∠MBG, △BNG≌△BCN,
∴∠GBN=∠CBN,
 ∵正方形BCDE,
∵正方形BCDE,
∴∠EBC=90°,
∴∴∠MBN=![]()
(2)不发生变化.


科目:初中数学 来源: 题型:
【题目】下列的真命题中,它的逆命题也是真命题的有 ( )
①两直线平行,同旁内角互补;②等边三角形是锐角三角形;③两个图形关于某直线成轴对称,则这两个图形是全等图形;④若a=b,则a2=b2;⑤等腰三角形两底角相等.
A.①②
B.①⑤
C.③④
D.④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果用有序数对(3,2)表示教室里第3列第2排的座位,则位于第5列第4排的座位应记作( )
A.(4,5)B.(5,4)C.(5,2)D.(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和 ![]() 个过滤网要花费
个过滤网要花费 ![]() 元,买
元,买 ![]() 个空气净化器和
个空气净化器和 ![]() 个过滤网要花费
个过滤网要花费 ![]() 元.
元.
(1)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(2)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买 ![]() 个空气净化器和
个空气净化器和 ![]() 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
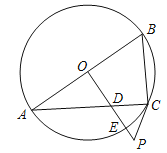
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,直线l1:y= ![]() x与直线l2:y=﹣x+6交于点A,l2与x轴交于B,与y轴交于点C.
x与直线l2:y=﹣x+6交于点A,l2与x轴交于B,与y轴交于点C.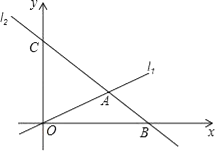
(1)求△OAC的面积;
(2)如点M在直线l2上,且使得△OAM的面积是△OAC面积的 ![]() ,求点M的坐标.
,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com