
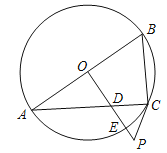
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
【答案】(1)证明见解析;(2)4-![]() .
.
【解析】
试题分析:(1)连接OC,由OB=OC及已知可得∠PCA=∠OCB.由直径所对的圆周角为直角有∠ACB=90°,从而可得∠OCP=90°,所以PC是⊙O的切线;(2)在Rt△PCO中,利用∠P的正切和正弦分别求得OC、OP的长,再根据PE=OP-OE计算即可.
试题解析:(1)连接OC. ∵OB=OC,∴∠ABC=∠OCB. 又∠PCA=∠ABC,∴∠PCA=∠OCB.∵AB为⊙O直径,∴∠ACB=90°. ∴∠ACO+∠OCB=90°,∴∠ACO+∠PCA=90°,即∠OCP=90°,∴PC是⊙O的切线;
(2)在Rt△PCO中,tan∠P=![]() ,∴OC=PCtan∠P=2tan60°=
,∴OC=PCtan∠P=2tan60°=![]() ,sin∠P=
,sin∠P=![]() ,∴OP=
,∴OP=![]() =
=![]() =4,∴PE=OP-OE=OP-OC=4-
=4,∴PE=OP-OE=OP-OC=4-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC , ∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF . 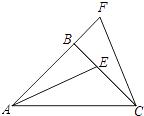
(1)求证:△ABE≌△CBF;
(2)若∠BAE=25°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
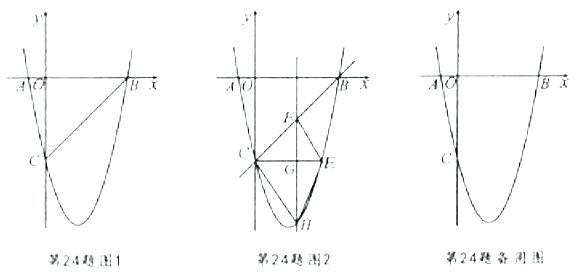
【题目】如图1,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)若点![]() 是
是![]() 轴上的一点,且以
轴上的一点,且以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
(3)如图2,![]() 轴玮抛物线相交于点
轴玮抛物线相交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的动点,过点
下方抛物线上的动点,过点![]() 且与
且与![]() 轴平行的直线与
轴平行的直线与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,试探究当点
,试探究当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 的面积最大,求点
的面积最大,求点![]() 的坐标及最大面积;
的坐标及最大面积;
(4)若点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 是该抛物线上的一点,在
是该抛物线上的一点,在![]() 轴,
轴,![]() 轴上分别找点
轴上分别找点![]() ,
,![]() ,使四边形
,使四边形![]() 的周长最小,求出点
的周长最小,求出点![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为直径的半圆弧上运动(点
为直径的半圆弧上运动(点![]() 不与点
不与点![]() 及
及![]() 的中点
的中点![]() 重合),连接
重合),连接![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为边在半圆同侧作正方形
为边在半圆同侧作正方形![]() ,过
,过![]() 点作
点作![]() 的切线交射线
的切线交射线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)探究:如左图,当![]() 动点在
动点在![]() 上运动时;
上运动时;
①判断![]() 是否成立?请说明理由;
是否成立?请说明理由;
②设![]() ,
,![]() 是否为定值?若是,求出该定值,若不是,请说明理由;
是否为定值?若是,求出该定值,若不是,请说明理由;
③设![]() ,
,![]() 是否为定值?若是,求出该定值,若不是,请说明理由;
是否为定值?若是,求出该定值,若不是,请说明理由;
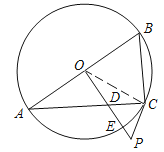
(2)拓展:如右图,当动点![]() 在
在![]() 上运动时;
上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道一次函数 ![]() 与
与 ![]() 的图象关于
的图象关于 ![]() 轴对称,所以我们定义:函数
轴对称,所以我们定义:函数 ![]() 与
与 ![]() 互为“镜子”函数.
互为“镜子”函数.
(1)请直接写出函数 ![]() 的“镜子”函数
的“镜子”函数
(2)如果一对“镜子”函数 ![]() 与
与 ![]() 的图象交于点
的图象交于点 ![]() ,且与
,且与 ![]() 轴交于
轴交于 ![]() 、
、 ![]() 两点,如图所示,若
两点,如图所示,若 ![]() ,且
,且 ![]() 的面积是
的面积是 ![]() ,求这对“镜子”函数的解析式.
,求这对“镜子”函数的解析式.
(3)若点 ![]() 是
是 ![]() 轴上的一个动点,当
轴上的一个动点,当 ![]() 为等腰三角形时,直接写出点
为等腰三角形时,直接写出点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC的三边a,b,c满足(ac)(a2+b2c2)=0,则△ABC是( )
A. 等腰三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在函数
在函数![]() (
(![]() )的图象上,点
)的图象上,点![]() 在直线
在直线![]() (
(![]() 为常数,且
为常数,且![]() )上,若
)上,若![]() ,
,![]() 两点关于原点对称,则称点
两点关于原点对称,则称点![]() ,
,![]() 为函数
为函数![]() ,
,![]() 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为
图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为
A.有![]() 对或
对或![]() 对 B.只有
对 B.只有![]() 对 C.只有
对 C.只有![]() 对 D.有
对 D.有![]() 对或
对或![]() 对
对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com