
【题目】我们知道一次函数 ![]() 与
与 ![]() 的图象关于
的图象关于 ![]() 轴对称,所以我们定义:函数
轴对称,所以我们定义:函数 ![]() 与
与 ![]() 互为“镜子”函数.
互为“镜子”函数.
(1)请直接写出函数 ![]() 的“镜子”函数
的“镜子”函数
(2)如果一对“镜子”函数 ![]() 与
与 ![]() 的图象交于点
的图象交于点 ![]() ,且与
,且与 ![]() 轴交于
轴交于 ![]() 、
、 ![]() 两点,如图所示,若
两点,如图所示,若 ![]() ,且
,且 ![]() 的面积是
的面积是 ![]() ,求这对“镜子”函数的解析式.
,求这对“镜子”函数的解析式.
(3)若点 ![]() 是
是 ![]() 轴上的一个动点,当
轴上的一个动点,当 ![]() 为等腰三角形时,直接写出点
为等腰三角形时,直接写出点 ![]() 的坐标.
的坐标.
【答案】
(1)解:根据题意,“镜子函数”为关于 ![]() 轴对称的两个函数,
轴对称的两个函数,
∴原函数的“镜子函数”为 ![]()
(2)解:根据题意, ![]() 和
和 ![]() 为一对“镜子函数”.
为一对“镜子函数”.
∴ ![]() ,即
,即 ![]() 为等腰直角三角形,
为等腰直角三角形,
即 ![]() ,
,
∴ ![]() ,
,
又∵ ![]() 且
且 ![]() ,
,
∴解得 ![]() ,
,
那么 ![]() 和
和 ![]()
(3)解:根据等腰三角形的性质,分情况,
∵ ![]() ,
, ![]() ,
,
∴以 ![]() 为顶点,则
为顶点,则 ![]() ,得
,得 ![]() ,
, ![]() ,
,
以 ![]() 为顶点,则
为顶点,则 ![]() ,得
,得 ![]() ,
,
以 ![]() 为顶点,则
为顶点,则 ![]() ,得
,得 ![]()
【解析】(1)根据“镜子”函数的定义,即可得出结果。
(2)(2)根据已知条件可证得△ABC是等腰直角三角形,得出OA=OB=OC,再根据△ABC的面积是8,就可得出点A、B、C的坐标,利用待定系数法即可求出这对“镜子函数”的解析式。
(3)根据等腰三角形的性质,分为三种情况讨论:当点A为顶点时;当点B为顶点时;当D为顶点时,根据AB、AO、BO的长,即可求出点D的坐标。


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC的( )
A. 三边垂直平分线的交点 B. 三条内角平分线的交点
C. 三条高的交点 D. 三条中线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
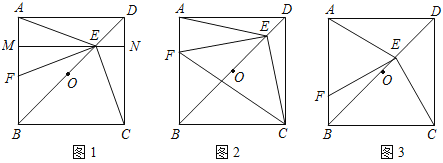
【题目】已知点O是正方形ABCD对角线BD的中点.
(1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.
①∠AEM=∠FEM; ②点F是AB的中点;
(2)如图2,若点E是OD上一点,点F是AB上一点,且使![]() ,请判断△EFC的形状,并说明理由;
,请判断△EFC的形状,并说明理由;
(3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当![]() 时,请猜想
时,请猜想![]() 的值(请直接写出结论).
的值(请直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
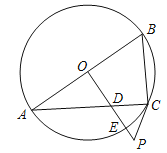
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题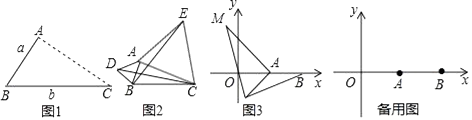
(1)问题
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)
(2)应用
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com