Question

16．如图，正方形OABC的边长为4，以O为圆心，EF为直径的半圆经过点A，连接AE，CF相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是（　　）

• A． 2$\sqrt{2}$π
• B． $\frac{8}{3}$π
• C． 4$\sqrt{5}$
• D． 6$\sqrt{2}$

Answer 1

分析 如图点P运动的路径是以G为圆心的弧$\widehat{EF}$，在⊙G上取一点H，连接EH、FH，只要证明∠EGF=90°，求出GE的长即可解决问题．

解答 解：如图，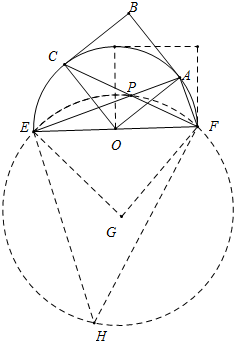
点P运动的路径是以G为圆心的弧$\widehat{EF}$，在⊙G上取一点H，连接EH、FH．
∵四边形AOCB是正方形，
∴∠AOC=90°，
∴∠AFP=$\frac{1}{2}$∠AOC=45°，
∵EF是⊙O直径，
∴∠EAF=90°，
∴∠APF=∠AFP=45°，
∴∠H=∠APF=45°，
∴∠EGF=2∠H=90°，
∵EF=4，GE=GF，
∴EG=GF=4$\sqrt{2}$，
∴$\widehat{EF}$的长=$\frac{90π•4\sqrt{2}}{180}$=2$\sqrt{2}$π．
故选：A．

点评 本题考查正方形的性质、旋转的性质、轨迹、圆等知识，解题的关键是正确发现轨迹的位置，学会添加辅助线，利用圆的有关性质解决问题，属于中考选择题中的压轴题．