
分析 为了使得二次函数y=mx2+(2m+1)x+m-1的图象总在x轴的下方,只须满足二次函数的抛物线开口向下且与x轴没有交点即可,据此列出不等关系即可求实数m的取值范围.
解答 解:由于二次函数y=mx2+(2m+1)x+m-1的图象总在x轴的下方,
令mx2+(2m+1)x+m-1=0,
则$\left\{\begin{array}{l}{m<0}\\{△=(2m+1)^{2}-4m(m-1)<0}\end{array}\right.$,
解得m<-$\frac{1}{8}$.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是掌握二次函数的图象在x轴的下方,则图象与x轴没有交点,此题难度不大.


科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中数学模拟试卷(四)(解析版) 题型:解答题
因式分【解析】
(1)4a2﹣16 ; (2)(x+2)(x+4)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
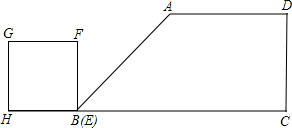 在直角梯形ABCD中,AD∥BC,∠D=90°,AD=6,BC=14,DC=4,边长为2的正方形EFGH自左向右在直线BC上以1个单位/秒的速度运动,H、E、B、C在同一直线上,从E、B重合到E、C重合时停止运动,若运动时间为t秒,连接AC.
在直角梯形ABCD中,AD∥BC,∠D=90°,AD=6,BC=14,DC=4,边长为2的正方形EFGH自左向右在直线BC上以1个单位/秒的速度运动,H、E、B、C在同一直线上,从E、B重合到E、C重合时停止运动,若运动时间为t秒,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
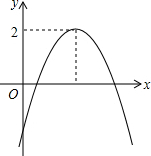 抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx-3=0的根的情况是( )
抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx-3=0的根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,DEFG为△ABC的内接矩形,∠A=90°,D在AB上,G在AC上,EF在斜边BC上,AB=3,AC=4.
如图,DEFG为△ABC的内接矩形,∠A=90°,D在AB上,G在AC上,EF在斜边BC上,AB=3,AC=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.
如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
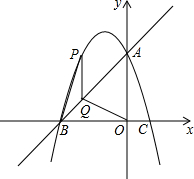 已知二次函数的图象与坐标轴交于A(0,3)、B(-3,0)、c(1,0).若点P是二次函数的图象上位于第二象限的点,过P作与y轴平行的直线与直线AB相交于点Q,则P点在何位置时,以线段BP、PO、OQ、QB围成的凹四边形的面积最大,并求最大值.
已知二次函数的图象与坐标轴交于A(0,3)、B(-3,0)、c(1,0).若点P是二次函数的图象上位于第二象限的点,过P作与y轴平行的直线与直线AB相交于点Q,则P点在何位置时,以线段BP、PO、OQ、QB围成的凹四边形的面积最大,并求最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com