
【题目】如图1,已知抛物线y=![]() x2—1与x轴交于A、B两点,顶点为C.
x2—1与x轴交于A、B两点,顶点为C.
(1)求A,B两点的坐标;
(2)若点P为抛物线上的一点,且S△APC=2,求点P的坐标;
(3)如图2,P(﹣2,﹣2),直线BD交抛物线于D,交y轴于M,连DP交抛物线于E,连BE交y轴于N,求CM ON的值.

图1 图2
【答案】(1)A(﹣2,0),B(2,0);(2)P(﹣4,3)或P(2,0);(3)2.
【解析】试题分析:(1)令y=0,则有0=![]() x2—1,解方程即可得;
x2—1,解方程即可得;
(2)在y轴正半轴上取一点M使S△ACM=2,则可得M(0,1),过M作AC的平行线与抛物线的交点即为满足条件的点;
(3)根据已知设yDP=kx+2k-2,D(x1,y1),E(x2,y2),联立 可得x1+x2=4k,x1·x2=4-8k,从而有
可得x1+x2=4k,x1·x2=4-8k,从而有![]() ,从而可得OM=
,从而可得OM=![]() ,同理:ON=
,同理:ON=![]() ,继而可得OM·ON=
,继而可得OM·ON=![]() .
.
试题解析:(1)令y=0,则有0=![]() x2—1,解得:x1=-2,x2=2,∴A(﹣2,0),B(2,0);
x2—1,解得:x1=-2,x2=2,∴A(﹣2,0),B(2,0);
(2)由y=![]() x2—1顶点为C,∴C(0,-1),
x2—1顶点为C,∴C(0,-1),
在y轴正半轴上取一点M使S△ACM=2,
∵A(-2,0),∴M(0,1),
∵A(-2,0),C(0,-1),
∴直线AC:y=![]() ,
,
过M作AC的平行线MP,则直线MP:y=![]() ,
,
解方程组 得:
得: ![]() ,
,
∴P(﹣4,3)或P(2,0);

(3)设yDP=kx+2k-2,D(x1,y1),E(x2,y2),
联立 得x2-4kx-8k+4=0,∴x1+x2=4k,x1·x2=4-8k,
得x2-4kx-8k+4=0,∴x1+x2=4k,x1·x2=4-8k,
![]() ,
,
当x=0时,OM= ,
,
同理:ON=![]() ,
,
所以OM·ON=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF、CF.

(1)如图1, 当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中![]() 为锐角,图2中
为锐角,图2中![]() 为直角,图3中
为直角,图3中![]() 为钝角).
为钝角).

在△ABC的边BC上取![]() ,
, ![]() 两点,使
两点,使![]() ,则
,则![]() ∽
∽![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,进而可得
,进而可得![]()
![]() ;(用
;(用![]() 表示)
表示)
若AB=4,AC=3,BC=6,则![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(t,0)是x轴上的动点,Q(0,2t)是y轴上的动点.若线段PQ与函数y=﹣|x|2+2|x|+3的图象只有一个公共点,则t的取值是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
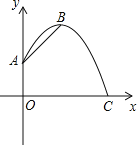
【题目】一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线与y轴成45°角,水流最高点B比喷头A高2米.
(1)求水流落地点C到O点的距离;
(2)若水流的水平位移s(米)(抛物线上两对称点之间的距离)与水流的运动时间(t秒)之间的函数关系为t= 0.8s,求共有几秒钟,水流高度不低于2米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小区:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据
成绩x(分) | 60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 |
甲小区 | 2 | 5 | a | b |
乙小区 | 3 | 7 | 5 | 5 |
分析数据
统计量 | 平均数 | 中位数 | 众数 |
甲小区 | 85.75 | 87.5 | c |
乙小区 | 83.5 | d | 80 |
应用数据
(1)填空:a= ,b= ,c= ,d= ;
(2)若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=![]() ,BE=
,BE=![]() .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
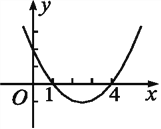
【题目】已知二次函数y=ax2-5x+c的图象如图所示.
(1)试求该二次函数的解析式和它的图象的顶点坐标;
(2)观察图象回答,x何值时y的值大于0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com