
分析 (1)根据关于x轴对称的点的横坐标相同,纵坐标互为相反数即可解决问题.
(2)点P关于直线y=x的对称点P′,作PE⊥y轴于E,P′F⊥x轴于F.构造全等三角形解决问题即可.
(3)分两种情形讨论即可.
(4)如图,△PQO是等边三角形时,点Q在x轴上,Q(2,0);△OPQ′是等边三角形时,P与Q′关于y轴对称,Q′(-1,$\sqrt{3}$).
(5)分两种情形讨论即可.
解答 解:(1)点P的坐标为(1,$\sqrt{3}$),点P关于x轴的对称点的坐标为(1,-$\sqrt{3}$),
故答案为(1,-$\sqrt{3}$).
(2)如图,点P关于直线y=x的对称点P′,作PE⊥y轴于E,P′F⊥x轴于F.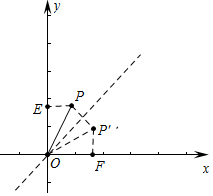
由△OPE≌△OP′F,可知PE=P′F=1,OE=OF=$\sqrt{3}$,
∴P′($\sqrt{3}$,1).
故答案为($\sqrt{3}$,1).
(3)如图观察图象可知,线段OP绕原点O旋转90°得到线段OB,则点B的坐标为($\sqrt{3}$,-1)或(-$\sqrt{3}$,1).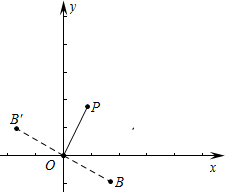
故答案为($\sqrt{3}$,-1)或(-$\sqrt{3}$,1).
(4)如图,△PQO是等边三角形时,点Q在x轴上,Q(2,0);△OPQ′是等边三角形时,P与Q′关于y轴对称,Q′(-1,$\sqrt{3}$).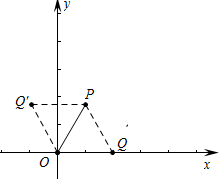
∴满足条件的点Q坐标(2,0)或(-1,$\sqrt{3}$).
故答案为(2,0)或(-1,$\sqrt{3}$).
(5)如图,①当∠AOP=90°,OP=OA时,A(-$\sqrt{3}$,1),
②当∠A′PO=90°,PA′=PO时,A′(-$\sqrt{3}$+1,1+$\sqrt{3}$).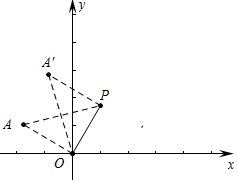
故答案为(-$\sqrt{3}$,1)或(-$\sqrt{3}$+1,1+$\sqrt{3}$).
点评 本题考查全等三角形的判定和性质、坐标与图形的变化、等边三角形的性质、旋转变换等知识,解题的关键是灵活运用所学知识解决问题,学会添加辅助线构造全等三角形解决问题,属于中考常考题型.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
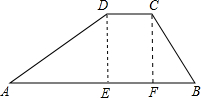 如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.
如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
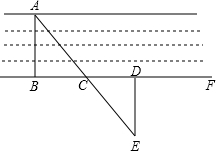 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线,并在这条垂线上取一点E,使A、C、E在一条直线上(如图所示),测得ED的长就是A、B之间的距离,请你说明理由.
如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线,并在这条垂线上取一点E,使A、C、E在一条直线上(如图所示),测得ED的长就是A、B之间的距离,请你说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.5千米 | B. | 1.5千米 | C. | 2.4千米 | D. | 14.9千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
| 优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com