
| 优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
| 优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
分析 (1)根据134<180可知第一次购物没有优惠;根据490>450可知第二次所购物品的原价超过500元,设小欣妈妈第二次所购物品的原价为x元,根据支付钱数=90%×500+超过500元的钱数×80%即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据支付钱数=90%×500+超过500元的钱数×80%算出将两次购买的物品一次全部买清所需钱数,将其与两次购物钱数相加做比较后即可得出结论.
解答 解:(1)∵第一次付了134元<200×90%=180元,
∴第一次购物不享受优惠,即所购物品的原价为134元;
②∵第二次付了490元>500×90%=450元,
∴第二次购物享受了500元按9折优惠,超过部分8折优惠.
设小欣妈妈第二次所购物品的原价为x元,
根据题意得:90%×500+(x-500)×80%=490,
得x=550.
答:小欣妈妈两次购物时,所购物品的原价分别为134元、550元.
(2)500×90%+(550+134-500)×80%=597.2(元),
又134+490=624(元),
∵597.2<624,
∴她将这两次购物合为一次购买更节省.
点评 本题考查了一元一次方程的应用,根据数量关系列出一元一次方程(或列式计算)是解题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
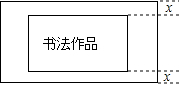 如图,现有一幅书法作品(图中阴影部分所示)需要装裱,已知该书法作品的长为50cm,宽为30cm,上、下边衬等宽、左、右边衬等宽,并且上、下边衬的宽与左、右边衬的宽比为1:2,已知装裱后的作品的面积为2800cm2.
如图,现有一幅书法作品(图中阴影部分所示)需要装裱,已知该书法作品的长为50cm,宽为30cm,上、下边衬等宽、左、右边衬等宽,并且上、下边衬的宽与左、右边衬的宽比为1:2,已知装裱后的作品的面积为2800cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
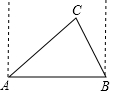 某次军事演习中,有三艘军舰在同一时刻向指挥所报告:A军舰说B军舰在它的正东方向,C军舰在它的北偏东60°方向;B军舰说C军舰在它的北偏西30°方向,C军舰说它到B军舰的距离比它到A军舰的距离近30海里,求A,B军舰的距离?(结果精确到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某次军事演习中,有三艘军舰在同一时刻向指挥所报告:A军舰说B军舰在它的正东方向,C军舰在它的北偏东60°方向;B军舰说C军舰在它的北偏西30°方向,C军舰说它到B军舰的距离比它到A军舰的距离近30海里,求A,B军舰的距离?(结果精确到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.
如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
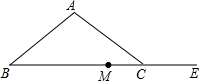 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com