
【题目】如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.
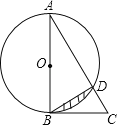
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]() π﹣
π﹣![]() .
.
【解析】
试题分析:(1)求出∠ADB的度数,求出∠ABD+∠DBC=90°,根据切线判定推出即可;
(2)分别求出等边三角形DOB面积和扇形DOB面积,即可求出答案.
(1)证明:∵AB为⊙O直径,
∴∠ADB=90°,
∴∠BAC+∠ABD=90°,
∵∠DBC=∠BAC,
∴∠DBC+∠ABD=90°,
∴AB⊥BC,
∵AB为直径,
∴BC是⊙O切线;
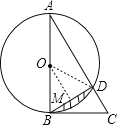
(2)解:连接OD,过O作OM⊥BD于M,
∵∠BAC=30°,
∴∠BOD=2∠A=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴OB=BD=OD=2,
∴BM=DM=1,
由勾股定理得:OM=![]() ,
,
∴阴影部分的面积S=S扇形DOB﹣S△DOB=![]() ﹣
﹣![]() ×2×
×2×![]() =
=![]() π﹣
π﹣![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】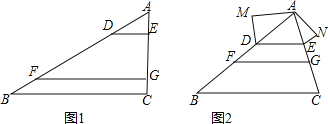
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= ,![]() = .
= .
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
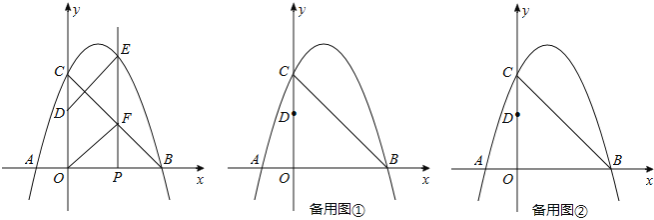
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A. 0是正数也是有理数 B. 两数之积为正,这两数同为正
C. 几个数相乘,积的符号由负因数的个数决定 D. 互为相反数的两个数的绝对值相等
查看答案和解析>>
科目:初中数学 来源: 题型:
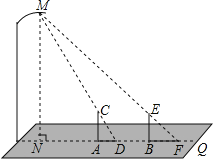
【题目】晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com