
【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为![]() .
.
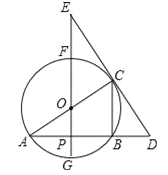
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:AP=BP=![]() AB=2;
AB=2;
(3)如果tan∠E=![]() ,求DE的长.
,求DE的长.
【答案】(1)AP=CB=2(2)(2)AP=BP=![]() AB=2;
AB=2;
(3)DE=![]() .
.
【解析】
试题分析:(1)根据圆周角定理由AC为直径得∠ABC=90°,在Rt△ABC中,根据勾股定理可计算出BC=2,再根据垂径定理由直径FG⊥AB得到AP=BP=![]() AB=2;
AB=2;
(2)易得OP为△ABC的中位线,则OP=![]() BC=1,再计算出
BC=1,再计算出![]() ,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;
,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;
(3)根据平行线的性质由BC∥EP得到∠DCB=∠E,则tan∠DCB=tan∠E=![]() ,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=
,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=![]() ,然后根据平行线分线段成比例定理得
,然后根据平行线分线段成比例定理得![]() ,再利用比例性质可计算出DE=
,再利用比例性质可计算出DE=![]() .
.
试题解析:(1)解:∵AC为直径,
∴∠ABC=90°,
在Rt△ABC中,AC=2![]() ,AB=4,
,AB=4,
∴BC=![]() =2,
=2,
∵直径FG⊥AB,
∴AP=BP=![]() AB=2;
AB=2;
(2)证明∵AP=BP,AO=OC
∴OP为△ABC的中位线,
∴OP=![]() BC=1,
BC=1,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∵∠EOC=∠AOP,
∴△EOC∽△AOP,
∴∠OCE=∠OPA=90°,
∴OC⊥DE,
∴DE是⊙O的切线;
(3)解:∵BC∥EP,
∴∠DCB=∠E,
∴tan∠DCB=tan∠E=![]()
在Rt△BCD中,BC=2,tan∠DCB=![]() =
=![]() ,
,
∴BD=3,
∴CD=![]() ,
,
∵BC∥EP,
∴![]() ,即
,即![]() ,
,
∴DE=![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小明在一块玻璃上画上了一幅画,然后用手电筒照着这块玻璃,将画映到雪白的墙上,这时我们认为玻璃上的画和墙上的画是位似图形.请你再举出一些生活中的位似图形来?并说明一对对应线段的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题:①对顶角相等;②内错角相等;③平行于同一条直线的两条直线互相平行; ④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等.其中真命题的是__________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在用摸球试验来模拟6人中有2人生肖相同的概率的过程中,有如下不同的观点,其中正确的是( )
A. 摸出的球不能放回 B. 摸出的球一定要放回
C. 可放回,可不放回 D. 不能用摸球试验来模拟此事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com