
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据合并同类项法则:只把系数相加,字母部分不变可得①错误;根据积的乘方运算法则:把积的每个因式分别乘方,再把幂相乘可得②正确;根据二次根式加减的计算法则可得③错误,根据a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数),a0=1(a≠0)计算可得④错误.
解答 解:①2ab+3ab=5ab,故原题计算错误;
②(-5a3)2=25a6,正确;
③$\sqrt{x+y}$无法计算,故原题计算错误;
④$\sqrt{12}$+($\frac{1}{3}$)-1-(π-3.14)0-|$\sqrt{3}$-2|
=2$\sqrt{3}$+3-1-(2-$\sqrt{3}$)
=3$\sqrt{3}$,故原题错误.
故选:A.
点评 此题主要考查了整式的混合运算以及合并同类项法则以及积的乘方运算法则和零指数以及负整数指数幂的性质等知识,正确掌握运算法则是解题关键.


科目:初中数学 来源: 题型:解答题
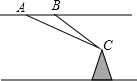 如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,飞机的飞行高度为2500米,在A点处测得某电视塔尖点C的俯角为30°,保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°.请计算电视塔的高度(结果保留整数,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
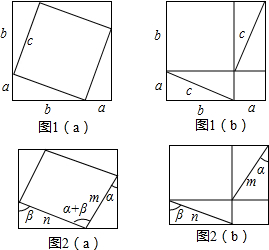
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
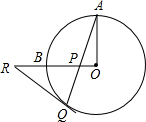 如图,OA、OB是⊙O的两条互相垂直的半径,P为OB上任一点,AP的延长线交⊙O于点Q,过点Q作⊙O的切线交OB的延长线于点R,求证:RP=RQ.
如图,OA、OB是⊙O的两条互相垂直的半径,P为OB上任一点,AP的延长线交⊙O于点Q,过点Q作⊙O的切线交OB的延长线于点R,求证:RP=RQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
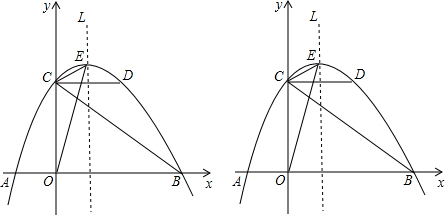
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com