
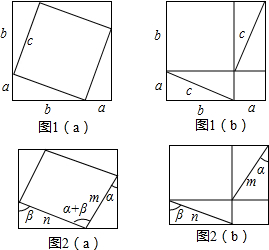
分析 根据平行四边形的面积公式求出图2(a)中?ABCD的面积,根据矩形的面积公式求出图2(b)中矩形ABCD与CEFG的面积,由图2(a)与图2(b)中空白部分的面积相等即可证明sin(α+β)=sinαcosβ+cosαsinβ.
解答 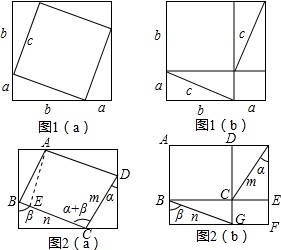 解:如图2(a),原来内部的正方形变成了一个平行四边形,m,n为相邻两边,其夹角为α+β,
解:如图2(a),原来内部的正方形变成了一个平行四边形,m,n为相邻两边,其夹角为α+β,
作?ABCD的高AE,则AE=AB•sinB=msin(180°-α-β)=msin(α+β),
则S?ABCD=BC•AE=n•msin(α+β)=mnsin(α+β).
如图2(b),原来的两个小正方形变成了两个矩形ABCD与CEFG,
则S矩形ABCD=BC•AB=nsinβ•mcosα=mncosαsinβ,
S矩形CEFG=CE•CG=msinα•ncosβ=mnsinαcosβ,
∵图2(a)与图2(b)中空白部分的面积相等,
∴mnsin(α+β)=mncosαsinβ+mnsinαcosβ,
化简得sin(α+β)=sinαcosβ+cosαsinβ.
点评 本题考查了解直角三角形,图形面积的计算,理解两幅图分别“压扁”成图2(a)和图2(b)后的形状得出它们空白部分的面积相等是解题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com